Силы трения
Силы трения всегда направлены вдоль соприкасающихся поверхностей противоположно движению тела. При изменении направления скорости изменяется направление сил трения.
Силы трения, как и силы упругости, имеют электромагнитную природу. Они возникают вследствие взаимодействия между атомами и молекулами соприкасающихся тел.
Силы трения отличаются от гравитационных сил и сил упругости тем, что эти силы зависят не только от конфигурации тел, т. е. от их взаимного расположения, но также еще от относительных скоростей взаимодействующих тел.
Виды трения
Если силы трения действуют между различными соприкасающимися телами (например, между телом и плоскостью, по которой оно движется или находится в покое), то такое трение называется внешним. Чисто внешнее трение является сухим трением, оно возникает в том случае, если между телами отсутствует слой смазки.
Силы сухого трения существенно зависят от степени обработки соприкасаемых поверхностей, их чистоты и относительной скорости. Силы сухого трения возникают не только при скольжении одного тела по поверхности другого, но и при попытке вызвать такое скольжение. Сила трения, которая существует между телами, которые соприкасаются, но не движутся под действием приложенной силы, носит название силы трения покоя.
В общем случае выделяют три вида внешнего трения: трение покоя, трение скольжения и трение качения.
Экспериментально установлено, что сила трения не зависит от площади поверхности, вдоль которой тела соприкасаются, и пропорциональна силе нормального давления, с которой одно тело действует на другое:
![]()
Постоянная ![]() называется коэффициентом трения и зависит от природы и состояния трущихся поверхностей.
называется коэффициентом трения и зависит от природы и состояния трущихся поверхностей.
В некоторых ситуациях трение является полезным. Например, при отсутствии трения невозможными были бы ходьба человека по земле, движение автотранспортных средств. Однако, в некоторых случаях трение вредно. Оно приводит к износу трущихся деталей механизмов, дополнительному расходу горючего на транспорте. В подобных случаях с трением борются путем применения различных смазок (так называемых жидкостных или воздушных подушек) или замены скольжения качением, поскольку трение качения характеризуется значительно меньшими силами по сравнению с трением скольжения.
Примеры решения задач
| Задание | Через сколько времени после начала аварийного торможения остановится автобус, движущийся со скоростью 12 м/с, если коэффициент трения при аварийном торможении равен 0,4? |
| Решение | Выполним рисунок и укажем все силы, действующие на автобус.
При аварийном торможении на автобус действуют сила тяжести 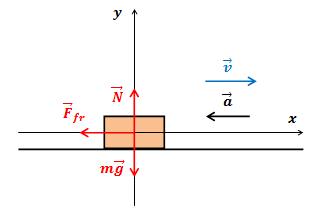
Выберем систему координат, как показано на рисунке, и спроектируем это векторное равенство на оси координат: Из второго уравнения: Сила трения: Подставив выражение для силы трения в первое уравнение, получим: или При торможении до полной остановки скорость автобуса падает от значения Приравнивая правые части соотношений для ускорения автобуса при аварийном торможении, получим: откуда время до полной остановки автобуса: Ускорение свободного падения Подставив в формулу численные значения физических величин, вычислим: |
| Ответ | Автобус остановится через |
| Задание | Небольшое тело положили на наклонную плоскость, составляющую угол |
| Решение | Выполним рисунок и укажем все силы, действующие на тело.
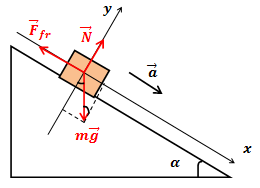
На тело действуют сила тяжести Выберем систему координат, как показано на рисунке, и спроектируем это векторное равенство на оси координат: Из второго уравнения: Сила трения: Подставив выражение для силы трения в первое уравнение, получим: откуда ускорение тела: Тело из состояния покоя начало двигаться равноускоренно, поэтому за время Подставив в эту формулу выражение для ускорения, получим: Ускорение свободного падения Вычислим: |
| Ответ | Тело пройдет расстояние 14,7 м. |











