Смещение точки. Амплитуда колебаний
Амплитуда колебаний — это абсолютная величина максимального отклонения колеблющейся точки от положения равновесия.
Амплитуда численно равна наибольшему смещению (рис.1).
В системе СИ единицей измерения смещения и амплитуды является метр.
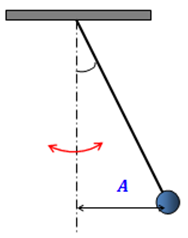
Рис.1 . Амплитуда колебаний как максимальное смещение
На графике колебаний амплитуда определяется как максимальная ордината синусоидальной кривой (рис.2).
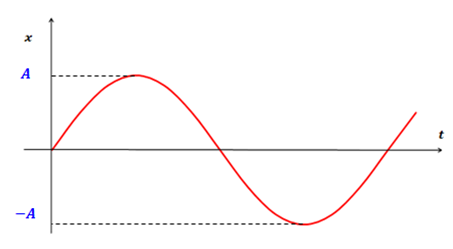
Рис.2. Определение по графику амплитуды колебаний
Примеры решения задач
| Задание | По графику колебаний определить начальное смещение тела, амплитуду и период колебания. Написать уравнение колебаний.
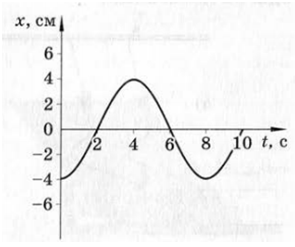
|
| Решение | Начальное смещение тела Период колебаний Определим циклическую частоту: Уравнение колебаний: Определим начальную фазу колебаний. Очевидно, что при откуда начальная фаза: |
| Ответ | Начальное смещение период колебаний 8 с, уравнение колебаний |
| Задание | Через какой минимальный промежуток времени после начала колебаний смещение точки из положения равновесия будет равно половине амплитуды, если период колебаний 24 с, а начальная фаза равна нулю? |
| Решение | Уравнение колебаний:
По условию начальная фаза Циклическая частота: Так как в искомый момент времени смещение равно половине амплитуды, можно записать: или откуда время: |
| Ответ | Искомое время |











