Пружинный маятник

Определения и формулы пружинного маятника

ОПРЕДЕЛЕНИЕ

Пружинный маятник – это колебательная система, состоящая из материальной точки и пружины (рис.1).

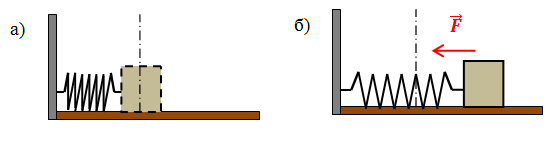
Рис.1. Пружинный маятник: а) в положении равновесия; б) в состоянии колебаний

Когда пружина не деформирована, тело находится в положении равновесия (рис.1,а). Если растянув или сжав пружину, вывести тело из положения равновесия, на него будет действовать сила упругости $\overline{F}$ со стороны деформированной пружины. Эта сила направлена к положению равновесия и в данном случае является возвращающей силой.

Сила упругости в пружинном маятнике

Сила упругости пропорциональна смещению тела (удлинению пружины):

$F=-kx,$

здесь $k$ — коэффициент жесткости пружины.

В положении, соответствующем максимальному отклонению тела от положения равновесия (смещение тела равно амплитуде колебаний) сила упругости максимальна, поэтому максимально и ускорение тела. По мере приближения тела к положению равновесия удлинение пружины уменьшается, и, следовательно, уменьшается ускорение тела, которое обусловлено силой упругости. Достигнув положения равновесия, тело не остановится, хотя в этот момент сила упругости равна нулю. Скорость тела в момент прохождения им положения равновесия имеет максимальное значение, и тело по инерции будет двигаться дальше, растягивая пружину. Возникающая при этом сила упругости будет тормозить тело, так как теперь она направлена в сторону, противоположную движению тела. Дойдя до крайнего положения, тело остановится и начнет движение в противоположном направлении. Движение тела будет повторяться в описанной последовательности.

Таким образом, причинами свободных колебаний пружинного маятника является сила упругости деформированной пружины (возвращающая сила) и инертность тела.

Период свободных колебаний пружинного маятника

Период свободных колебаний пружинного маятника определяется по формуле:

$T=2\pi \sqrt{\frac{m}{k}}$

Примеры решения задач

ПРИМЕР 1

Задание

На какое расстояние надо отвести от положения равновесия груз массой 640 г, закрепленный на пружине жесткостью 0,4 кН/м, чтобы он проходил положение равновесия со скоростью 1 м/с?

Решение

Движение пружинного маятника происходит по гармоническому закону:

$x=A\sin \left(\omega t+{\varphi }_0\right)$

Начальная фаза колебаний в данном случае равна нулю, поэтому можно записать:

$x=A\sin \omega t$

Положение равновесия тело проходит с максимальной скоростью. Найдем закон изменения скорости тела со временем:

$v=x'=A\omega \cos \omega t,$

откуда максимальное значение скорости:

$v_{max}=A\omega$

Период колебаний пружинного маятника определяется формулой:

$T=2\pi \sqrt{\frac{m}{k}}$

Циклическая частота:

$\omega =\frac{2\pi }{T}=\sqrt{\frac{k}{m}}$

Подставив значение циклической частоты в соотношение для максимальной скорости, получим:

$v_{max}=A\sqrt{\frac{k}{m}}$

откуда амплитуда колебаний маятника:

$A=v_{max}\sqrt{\frac{m}{k}}$

Переведем единицы в систему СИ: масса груза $m=640$ г $=0,64$ кг; коэффициент жесткости пружины $k=0,4$ кН/м $=400$ Н/м.

Вычислим:

$A=1\cdot \sqrt{\frac{0,64}{400}}=0,04\ m=4\ cm\$

Ответ

Груз нужно отвести на расстояние 4 см от положения равновесия.

ПРИМЕР 2

Задание

Если к некоторому грузу, колеблющемуся на пружине, подвесить гирю массой 100 г, то частота колебаний маятника уменьшится в 1,5 раза. Какой массы груз был первоначально подвешен к пружине?

Решение

Период колебаний пружинного маятника определяется формулой:

$T=2\pi \sqrt{\frac{m}{k}}$

Частота колебаний маятника:

$\nu =\frac{1}{T}=\frac{1}{2\pi }\sqrt{\frac{k}{m}}\$