Формулы приведения тригонометрических функций

Формулы, с помощью которых тригонометрические функции произвольного аргумента можно привести к функциям острого угла, называются формулами приведения тригонометрических функций. Эти формулы тригонометрии изучаются в 10 классе, их можно получить, используя формулы сложения и вычитания аргументов.

ПРИМЕР 1

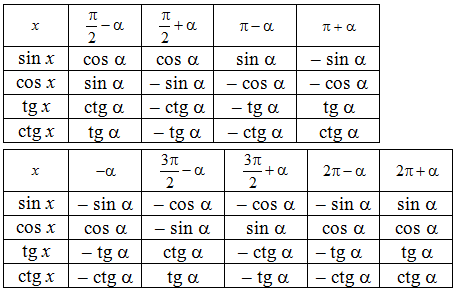
Задание	Упростить выражение $\sin \left( \frac{\pi }{2}-\alpha \right)+\cos \left( \pi +\alpha \right)$
Решение	Воспользуемся формулами приведения $\sin \left( \frac{\pi }{2}-\alpha \right)+\cos \left( \pi +\alpha \right)=\cos \alpha -\cos \alpha =0$
Ответ

ПРИМЕР 2

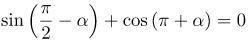Задание

Привести $\text{tg}\ \text{372}{{\text{8}}^{\circ }}$ к функции острого угла.

Решение

Так как функция $y=\text{tg}\ x$ является периодической с периодом $\pi ,$ то тангенсы углом, отличающихся друг от друга на число, кратное периоду – ${{180}^{\circ }}\cdot n$ – равны, то есть

$\text{tg}\ \text{372}{{\text{8}}^{\circ }}=\text{tg}\ \left( {{128}^{\circ }}+20\cdot {{180}^{\circ }} \right)=\text{tg}\ {{128}^{\circ }}$

Угол ${{128}^{\circ }}$ представим в виде следующей суммы:

${{128}^{\circ }}={{90}^{\circ }}+{{38}^{\circ }}$

то есть

$\text{tg}\ {{128}^{\circ }}=\text{tg}\ \left( {{90}^{\circ }}+{{38}^{\circ }} \right)$

Используя тот факт, что ${{90}^{\circ }}=\frac{\pi }{2}$ рад, на пересечении третьей строки и третьего столбца таблицы, приведенной выше, получаем:

$\text{tg}\ {{3728}^{\circ }}=\text{tg}\ \left( {{90}^{\circ }}+{{38}^{\circ }} \right)=-\text{ctg}\ {{38}^{\circ }}$

Ответ

$\text{tg}\ {{3728}^{\circ }}=-\text{ctg}\ {{38}^{\circ }}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Формулы приведения тригонометрических функций