Интегралы тригонометрических функций

Интеграл от синуса равен минус косинусу плюс константа интегрирования

$\int{\sin xdx}=-\cos x+C$

Интеграл от косинуса равен синусу плюс константа интегрирования

$\int{\cos xdx}=\sin x+C$

Интеграл от тангенса равен минус логарифму натуральному косинуса плюс константа интегрирования

$\int{\text{tg}\,xdx}=-\ln \left| \cos x \right|+C$

Интеграл от котангенса равен логарифму натуральному синуса плюс константа интегрирования

$\int{\text{ctg}\,xdx}=\ln \left| \sin x \right|+C$

Примеры решения задач

ПРИМЕР 1

Задание

Найти интеграл $\int{\left( 2\sin x+x \right)dx}$

Решение

Согласно свойствам интеграла, интеграл суммы равен сумме интегралов и постоянный множитель можно выносить за знак интеграла. Тогда заданный интеграл перепишется в виде:

$\int{\left( 2\sin x+x \right)dx}=2\int{\sin xdx}+\int{xdx}$

Интеграл от первого слагаемого

$\int{\sin xdx}=-\cos x+C$

а от второго, как от степенной функции,

$\int{{{x}^{n}}dx}=\frac{{{x}^{n+1}}}{n+1}+C$

При $n=1$ будем иметь:

$\int{xdx}=\frac{{{x}^{2}}}{2}+C$

Итак, искомый интеграл

$\int{\left( 2\sin x+x \right)dx}=2\cdot \left( -\cos x \right)+\frac{{{x}^{2}}}{2}+C=-2\cos x+\frac{{{x}^{2}}}{2}+C$

Ответ

ПРИМЕР 2

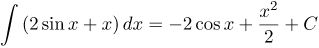Задание

Доказать, что $\int{\text{ctg}\,xdx}=\ln \sin x+C$

Решение

Выведем записанную формулу. Для этого преобразуем подынтегральное выражение и применим метод подстановки для нахождения неопределенного интеграла:

$\int{\text{ctg}\,xdx}=\int{\frac{\cos x}{\sin x}dx}\ \left\| \begin{matrix} \sin x=t \\ \cos xdx=dt \\ \end{matrix} \right\|=\int{\frac{dt}{t}}=\ln \left| t \right|+C=\ln \left| \sin x \right|+C$

Что и требовалось доказать.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Интегралы тригонометрических функций

Примеры решения задач