Примеры решения производных тригонометрических функций
Теория по производным тригонометрических функций
Производные тригонометрических функций равны соответственно:
![]()
Используя эти производные и правила дифференцирования, выведем формулу для нахождения производной функции ![]() . Представим эту функции как
. Представим эту функции как ![]() , тогда
, тогда
![]()
Далее по правилу дифференцирования частного, получим
![]()
Учитывая, что в числителе у нас записано основное тригонометрическое тождество, окончательно получим:
![]()
Аналогично можно вывести формулу для котангенса
![]()
Примеры
| Задание | Найти производную функции |
| Решение | Производная разности равна разности производных
Преобразуем полученное выражение, используя основное тригонометрическое тождество и формулы двойного угла: |
| Ответ | 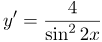 |
| Задание | Найти производную функции |
| Решение | Заданная функция является сложной и её производная равна произведению производной от косинуса на производную от его аргумента:
|
| Ответ |
| Задание | Найти производную функции |
| Решение | Заданная функция является сложной, поэтому сначала находим производную от синуса (косинус того же аргумента) и так как аргумент есть выражением более сложным, чем просто |
| Ответ |  |
| Задание | Найти производную от функции |
| Решение | Данная функция является сложной функции. По правилу нахождения производной сложной функции, сначала, найдем производную от неё как от степенной функции, а затем найдем производную от аргумента. В данном случае, аргументом есть функция |
| Ответ |
| Задание | Найти производную функции
|
| Решение | Перепишем заданную функцию следующим образом:
Производную от этой функции будем находить по правилу нахождения производной сложной функции. Сначала как от степенной функции, а затем – от аргумента как от тригонометрической. Получим: Преобразуем полученное выражение, представляя |
| Ответ | 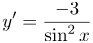 |











