Примеры интегрирования тригонометрических функций
Чтобы привести интеграл, содержащий тригонометрические функции, к интегралу, который выражается в элементарных функциях, используют тригонометрические формулы, такие как: формулы понижения степени, формулы произведения тригонометрических функций, формулы двойного угла и т.д. В случае если, интеграл не может быть приведен к интегралу, который выражается в элементарных функциях, используют метод замены переменной или внесения под знак дифференциала.
| Задание | Найти неопределенный интеграл
|
| Решение | Понизим степень синуса, используя тригонометрическую формулу понижения степени, получим
Во втором интеграле внесем |
| Ответ | 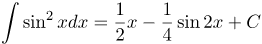 |
| Задание | Найти неопределенный интеграл
|
| Решение | Преобразуем подынтегральное выражение, используя формулу произведения тригонометрических функций:
Учитывая, что синус функция нечетная, получим: |
| Ответ | 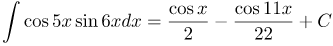 |
| Задание | Найти интеграл тригонометрической функции
|
| Решение | В подынтегральном выражении выделим первую степень косинуса, получим:
Преобразуем подынтегральное выражение, используя основное тригонометрическое тождество: Далее внесем косинус под знак дифференциала |
| Ответ | 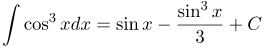 |
| Задание | Найти интеграл
|
| Решение | Преобразуем подынтегральное выражение
Введем замену Делая обратную замену |
| Ответ | 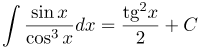 |
| Задание | Вычислить интеграл тригонометрической функции
|
| Решение | Вычислять этот интеграл будем, используя метод замены переменной. Введем замену в исходный интеграл
Вычислим новые пределы интегрирования Подставляя, введенную замену, в исходный интеграл, получим: |
| Ответ | 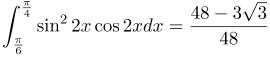 |






![Rendered by QuickLaTeX.com \[ \int _{\frac{\pi}{6}}^{\frac{\pi}{4}} \sin ^{2} 2x \cos 2x dx \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-edc5bdf53b0e2bccf1c92e55652899b9_l3.png)
![Rendered by QuickLaTeX.com \[ \int _{\frac{\pi}{6}}^{\frac{\pi}{4}} \sin ^{2} 2x \cos 2x dx = \int _{\frac{\sqrt{3}}{2}}^{1} t^{2} \frac{dt}{2} = \frac{1}{2} \int _{\frac{\sqrt{3}}{2}}^{1} t^{2} dt = \frac{1}{2} \cdot \frac{t^{3}}{3} \bigg| _{\frac{\sqrt{3}}{2}}^{1} = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-963f98657ff2ddd4570263c455ce5a32_l3.png)
![Rendered by QuickLaTeX.com \[ = \frac{1}{6} \left( 1^{3} - \left( \frac{\sqrt{3}}{2} \right)^{3} \right) = \frac{48 - 3 \sqrt{3}}{48} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-75304170ba5cc6d8e3dda40772569f9a_l3.png)





