Примеры интегрирования иррациональных функций
Иррациональной называется функция, у которой переменная находится под знаком корня. Не для всякой иррациональной функции можно найти первообразную в виде элементарной функции. Для нахождения таких интегралов чаще всего используют метод замены переменной.
| Задание | Найти неопределенный интеграл
|
| Решение | Константу можно вынести за знак интеграла
Полученный интеграл является табличным («длинный логарифм») и равен |
| Ответ | 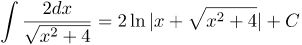 |
| Задание | Найти интеграл иррациональной функции
|
| Решение | Введем замену Сделаем обратную замену |
| Ответ | 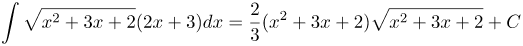 |
| Задание | Найти неопределенный интеграл
|
| Решение | Запишем степени переменных в подынтегральном выражении следующим образом
Поделим почленно числитель на знаменатель, получим |
| Ответ | 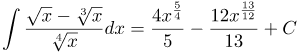 |
| Задание | Найти неопределенный интеграл
|
| Решение | Введем замену Используя основное тригонометрическое тождество, получим: Применим формулу для понижения степени: Сделаем обратную замену |
| Ответ | 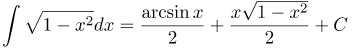 |
| Задание | Вычислить интеграл иррациональной функции
|
| Решение | Вынесем из под корня 9 и воспользуемся свойством определенного интеграла с симметричными пределами интегрирования
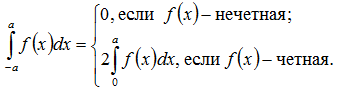
Получим: Введем замену переменной Пределы интегрирования изменятся следующим образом: при Преобразуем полученный интеграл, используя основное тригонометрическое тождество: Далее понизим степень косинуса: |
| Ответ | 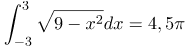 |






![Rendered by QuickLaTeX.com \[ \int \sqrt{x^{2}+3x+2} (2x+3) dx = \int \sqrt{t}dt = \frac{t^{\frac{3}{2}}}{\frac{3}{2}} + C = \frac{2t \sqrt{t}}{3} + C \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-66e8abda5b089da0a420a8d56820f8cf_l3.png)
![Rendered by QuickLaTeX.com \[ \int \frac{\sqrt{x} - \sqrt[3]{x}}{\sqrt[4]{x}} dx = \int \frac{x^{\frac{1}{2}} - x^{\frac{1}{3}}}{x^{\frac{1}{4}}} dx \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-575619d808dc6ca685db3aa7e9add6df_l3.png)
![Rendered by QuickLaTeX.com \[ \int \frac{\sqrt{x} - \sqrt[3]{x}}{\sqrt[4]{x}} dx = \int \frac{x^{\frac{1}{2}} - x^{\frac{1}{3}}}{x^{\frac{1}{4}}} dx = \int x^{\frac{1}{2} -\frac{1}{4}} dx - \int x^{\frac{1}{3} -\frac{1}{4}} dx = \int x^{\frac{1}{4}} dx - \int x^{\frac{1}{12}} dx = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9b7c88d5549468d07ea37512ccfef7e0_l3.png)
![Rendered by QuickLaTeX.com \[ = \frac{x^{\frac{1}{4}+1}}{\frac{1}{4}+1} - \frac{x^{\frac{1}{12}+1}}{\frac{1}{12}+1} + C = \frac{4 x^{\frac{5}{4}}}{5} - \frac{12 x^{\frac{13}{12}}}{13} + C \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-eab57a577f054b8612d5661ffb446148_l3.png)
![Rendered by QuickLaTeX.com \[ \int _{-3}^{3} \sqrt{9-x^{2}} dx = 6 \int _{0}^{3} \sqrt{1 - \frac{x^{2}}{9}} dx = 6 \int _{0}^{\frac{\pi}{2}} \sqrt{1 - \frac{9 \sin ^{2} t}{9}} \cdot 3 \cos t dt = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c6b76b37b057d48863a8acb472b58bcb_l3.png)
![Rendered by QuickLaTeX.com \[ \int _{-3}^{3} \sqrt{9-x^{2}} dx = 18 \int _{0}^{\frac{\pi}{2}} \cos ^{2} t dt = \frac{18}{2} \int _{0}^{\frac{\pi}{2}} (1+\cos 2t) dt = 9t \bigg| _{0}^{\frac{\pi}{2}} + \frac{9}{2} \cdot \sin 2t \bigg| _{0}^{\frac{\pi}{2}} = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-feb348d28028f0d7ebd1eeae1158d516_l3.png)





