Косинус угла

Определение и формула косинуса

ОПРЕДЕЛЕНИЕ

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к гипотенузе.

Рассмотрим прямоугольный треугольник $\Delta ABC, \angle C={{90}^{\circ }}, AB$ или $c$ – гипотенуза, а $AC$ или $b$ и $BC$ или $a$ – катеты прилежащие соответственно к острым углам $\alpha$ и $\beta$ (рис. 1).

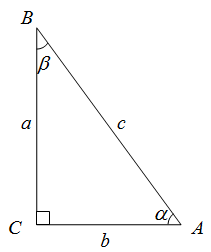
Рис. 1

В этих обозначениях косинусы острых углов запишутся следующим образом

$\cos \alpha =\frac{b}{c} \quad \cos \alpha =\frac{AC}{AB}$

$\cos \beta =\frac{a}{c} \quad \cos \beta =\frac{BC}{AB}$

Рассмотрим единичную тригонометрическую окружность с центром в начале координат. Выберем произвольный угол $\alpha$ (рис. 2), которому на единичной окружности соответствует точка $A \left( {{x}_{0}},{{y}_{0}} \right).$

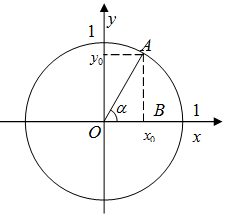
Рис. 2

Опустим перпендикуляр AB из точки A на ось $Ox.$ Тогда

$\cos \alpha =\frac{BO}{AO},$

учитывая, что радиус окружности $AO=1,$ то

$\cos \alpha =BO={{x}_{0}},$

то есть косинусом угла $\alpha$ есть абсцисса точки $A.$

Примеры решения задач

ПРИМЕР 1

Задание

В прямоугольном треугольнике один из острых углов равен ${{30}^{\circ }},$ а гипотенуза равна $2\sqrt{3}$ см. Найти катет, прилежащий к заданному углу.

Решение

Обозначим гипотенузу $c=2\sqrt{3},$ острый угол $\alpha ={{30}^{\circ }},$ тогда искомый прилежащий катет $b.$ По определению отношение прилежащего катета к гипотенузе равно косинусу. Тогда, во введенных обозначениях, это запишется следующим образом:

$\cos \alpha =\frac{b}{c}$

Выразим из этого соотношения искомый катет: $b=c\cdot \cos \alpha .$ Подставим в последнее равенство заданные значения, получим

$b=2\sqrt{3}\cdot \cos {{30}^{\circ }}\ \quad \Rightarrow \ \quad b=2\sqrt{3}\cdot \frac{\sqrt{3}}{2}\ \quad \Rightarrow \ \quad b=3 cm$

Ответ

$b=3$ см

ПРИМЕР 2

Задание

Один из катетов прямоугольного треугольника равен 3 см, а гипотенуза равна 6. Найти градусную меру угла между ними.

Решение

Обозначим заданный катет $a=3,$ а гипотенузу $c=6,$ тогда угол между ними обозначим $\beta .$ Отношение прилежащего к некоторому острому углу катета к гипотенузе равно косинусу этого угла. В веденных обозначениях это соотношение запишется следующим образом

$\cos \beta =\frac{a}{c}$

Подставим в это равенство заданные значения сторон, получим

$\cos \beta =\frac{3}{6}\ \quad \Rightarrow \ \quad \cos \beta =\frac{1}{2}\ \quad \Rightarrow \ \quad \beta ={{60}^{\circ }}$

Ответ

$\beta ={{60}^{\circ }}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Косинус угла

Определение и формула косинуса

Примеры решения задач