Тригонометрические функции
Определения и формулы всех тригонометрических функций
Рассмотрим произвольный прямоугольный треугольник ![]() , углы
, углы ![]() и
и ![]() – острые. (рис. 1). Тогда
– острые. (рис. 1). Тогда ![]() – гипотенуза (это сторона противолежащая прямому углу), самая длинная сторона в прямоугольном треугольнике. Катет
– гипотенуза (это сторона противолежащая прямому углу), самая длинная сторона в прямоугольном треугольнике. Катет ![]() – это катет, являющийся противолежащим по отношению к углу
– это катет, являющийся противолежащим по отношению к углу ![]() . Катет
. Катет ![]() – это катет, прилежащий к углу
– это катет, прилежащий к углу ![]() .
.
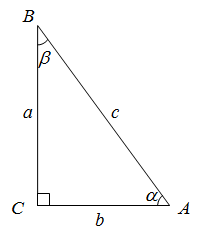
Рис. 1
![]()
Это отношение не зависит от выбора ![]() , содержащего угол
, содержащего угол ![]() , так как все такие треугольники подобны.
, так как все такие треугольники подобны.
Подробнее про синус угла читайте по ссылке.
![]()
Подробнее про косинус угла читайте по ссылке.
Замечание 1. Катет AC, прилежащий к углу ![]() , является противолежащим по отношению к углу
, является противолежащим по отношению к углу ![]() . Аналогично с катетом
. Аналогично с катетом ![]() , он противолежащий для угла
, он противолежащий для угла ![]() и прилежащий к углу
и прилежащий к углу ![]() . Таким образом, синус одного острого угла в треугольнике равен косинусу второго его острого угла, и наоборот:
. Таким образом, синус одного острого угла в треугольнике равен косинусу второго его острого угла, и наоборот:
![]()
![]()
Также тангенс выражается через косинус и синус следующим образом:
![]()
![]()
Котангенс выражается через косину и синус следующим образом:
![]()
Замечание 2. Котангенс одного острого угла в прямоугольном треугольнике равен тангенсу второго его острого угла, и наоборот:
![]()
Секансом угла ![]() называется отношение гипотенузы
называется отношение гипотенузы ![]() к прилежащему катету или
к прилежащему катету или
![]()
![]()
Косекансом угла ![]() называется отношение гипотенузы
называется отношение гипотенузы ![]() к противолежащему катету
к противолежащему катету ![]() или
или
![]()
Косеканс можно выразить через синус:
![]()
Примеры решения задач
| Задание | В прямоугольном треугольнике катеты имеют длины 4 см и 3 см. Вычислить значения всех тригонометрических функций для угла прилежащего к меньшему катету.
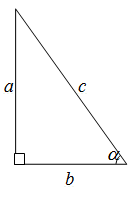
Рис. 2 |
| Решение | Сделаем рисунок (рис. 2). По условию, По определению, синус – это отношение противолежащего катета к гипотенузе: Косинус – это отношение прилежащего катета к гипотенузе Тангенс – это отношение противолежащего катета к прилежащему катету Котангенс – это отношение прилежащего катета к противолежащему катету Секанс – это отношение гипотенузы к прилежащему катету Косеканс – это отношение гипотенузы к противолежащему катету |
| Ответ | 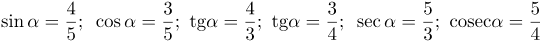 |
Примечание. Прямоугольный треугольник со сторонами 3, 4, 5 называется «египетским треугольником». Это простейший треугольник из Героновых треугольников – треугольников с целочисленными сторонами и площадями.
| Задание | В прямоугольном треугольнике гипотенуза и один из катетов равны соответственно 13 и 5 см. Найти значение косинуса, синуса, тангенса и котангенса для острых углов этого треугольника.
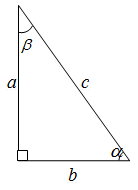
Рис. 3 |
| Решение | Рассматриваемый треугольник изображен на рисунке 3. По условию задачи гипотенуза c равна 13 см, а меньший катета Перейдем к нахождению значений тригонометрических функций. Согласно замечанию 1, Подставляя заданные значения длины сторон, получим По замечанию 2, |
| Ответ | 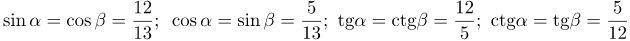 |











