Таблица значений тригонометрических функций

При решении математических задач часто используются тригонометрические функции, поэтому знание значений этих функций для часто используемых углов просто необходимо.

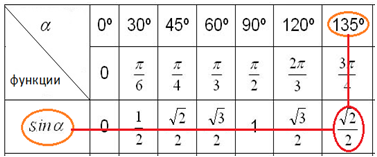
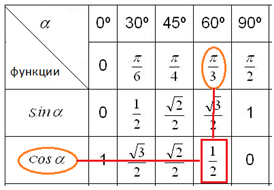
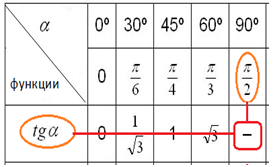
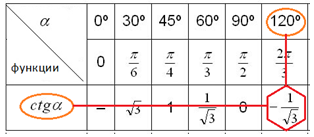
В приведенной ниже таблице записаны значения тригонометрических функций 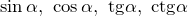$\sin \alpha , \ \cos \alpha , \ \text{tg} \alpha , \ \text{ctg} \alpha$ аргумент 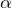$\alpha$ которых задан в градусах (в первой строке) и в радианах (во второй строке). Это позволяет перевести значение популярных углов из градусов в радианы. Значения тригонометрических функций стоят на пересечении строки функции и столбца искомого угла.

Значения тригонометрических функций чаще всего требуются при решении геометрических задач.

Примеры решения задач

ПРИМЕР 1

Задание	Определить значение $\sin {{135}^{\circ }}$
Решение	Воспользуемся таблицей значений тригонометрических функций. В строке значений угла $\alpha$ найдем указанный угол ${{135}^{\circ }}$ . В столбце функций находим заданную функцию $\sin \alpha$ . На пересечении этих строки и столбца находится искомое значение.
Ответ	$\sin {{135}^{\circ }}=\frac{\sqrt{2}}{2}$

ПРИМЕР 2

Задание	Определить значение $\cos \frac{\pi }{3}$
Решение	Для определения заданного значения воспользуемся таблицей значений тригонометрических функций. В строке значений угла $\alpha$ находим значение $\alpha =\frac{\pi }{3}$ . В столбце функций находим $\cos \alpha$ . Тогда на пересечении соответствующих столбца и строки лежит искомое значение $\cos \frac{\pi }{3}=\frac{1}{2}$ .
Ответ	$\cos \frac{\pi }{3}=\frac{1}{2}$

ПРИМЕР 3

Задание	С помощью таблицы значений тригонометрических функций определить значение $\text{tg}\frac{\pi }{2}$
Решение	В строке значений угла $\alpha$ находим значение $\frac{\pi }{2}$ . В столбце функций находим $\text{tg}\alpha$ . Тогда на пересечении строки, которая содержит $\text{tg}\alpha$ , и столбца, содержащего $\frac{\pi }{2}$ , находится искомое значение функции. Но там стоит прочерк, это значит, что $\text{tg}\frac{\pi }{2}$ не существует.
Ответ	$\text{tg}\frac{\pi }{2}$ не существует.

ПРИМЕР 4

Задание	Используя таблицу значений тригонометрических функций определить значение $\text{ctg}{{120}^{\circ }}$
Решение	В строке значений угла $\alpha$ находим ${{120}^{\circ }}$ . В столбце функций находим $\text{ctg}\alpha$ . На пересечении столбца соответствующего ${{120}^{\circ }}$ и строки соответствующей $\text{ctg}\alpha$ находим искомое значение функции $\text{ctg}{{120}^{\circ }}=-\frac{1}{\sqrt{3}}$ .
Ответ	$\text{ctg}{{120}^{\circ }}=-\frac{1}{\sqrt{3}}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Таблица значений тригонометрических функций

Примеры решения задач