Таблица Брадиса (синусы)

Таблица Брадиса для синусов позволяет найти значение синуса любого острого угла, содержащего целое число градусов и десятых долей градуса. Для нахождения значения синуса заданного угла, в первом столбце значений находится строка, соответствующая целому значению его градусов. Далее в первой строке находится столбец, соответствующий заданному значению минут. На пересечении строки градусов и столбца минут находится искомое значение синуса. Ниже приведены таблицы Брадиса для синусов и косинусов.

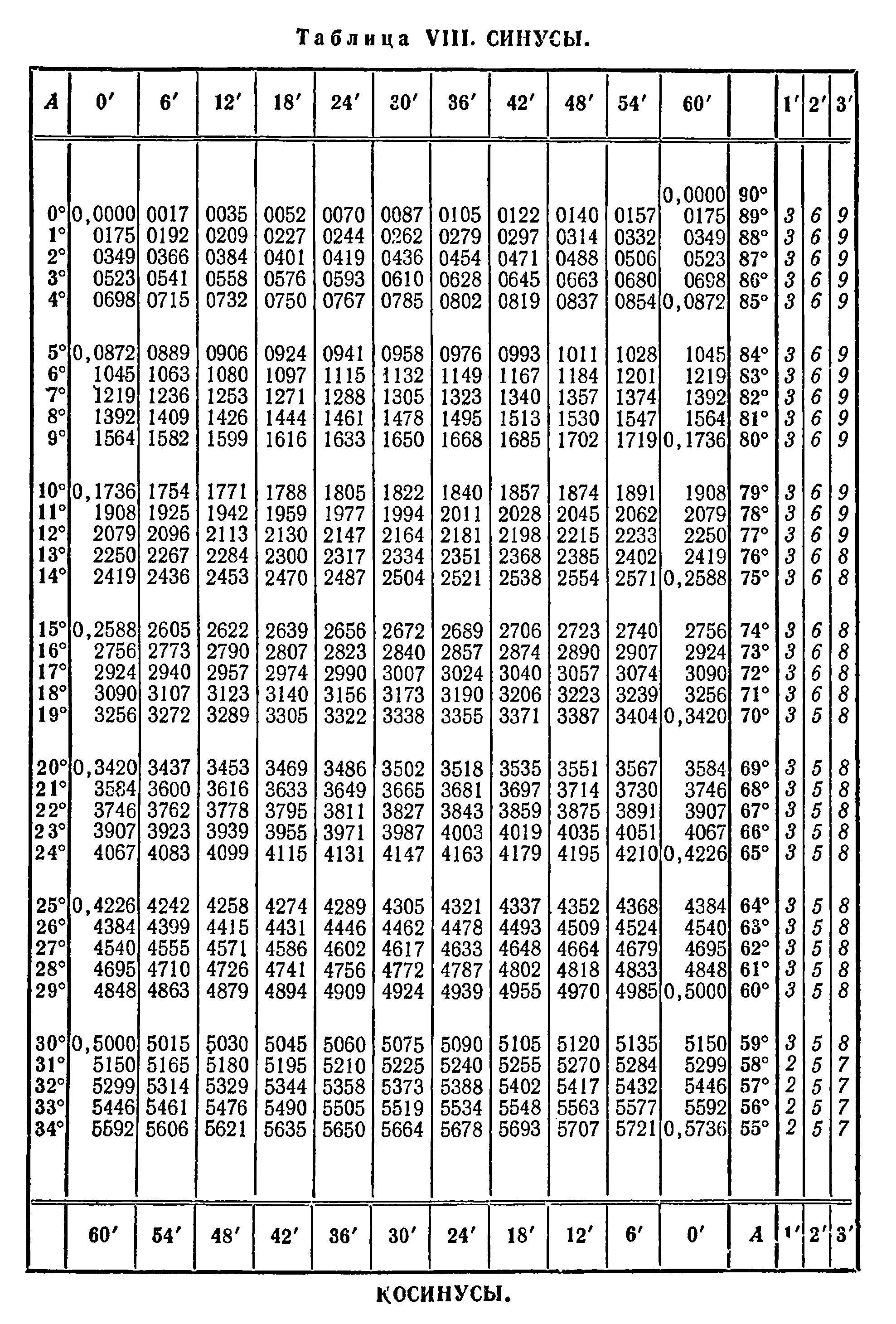
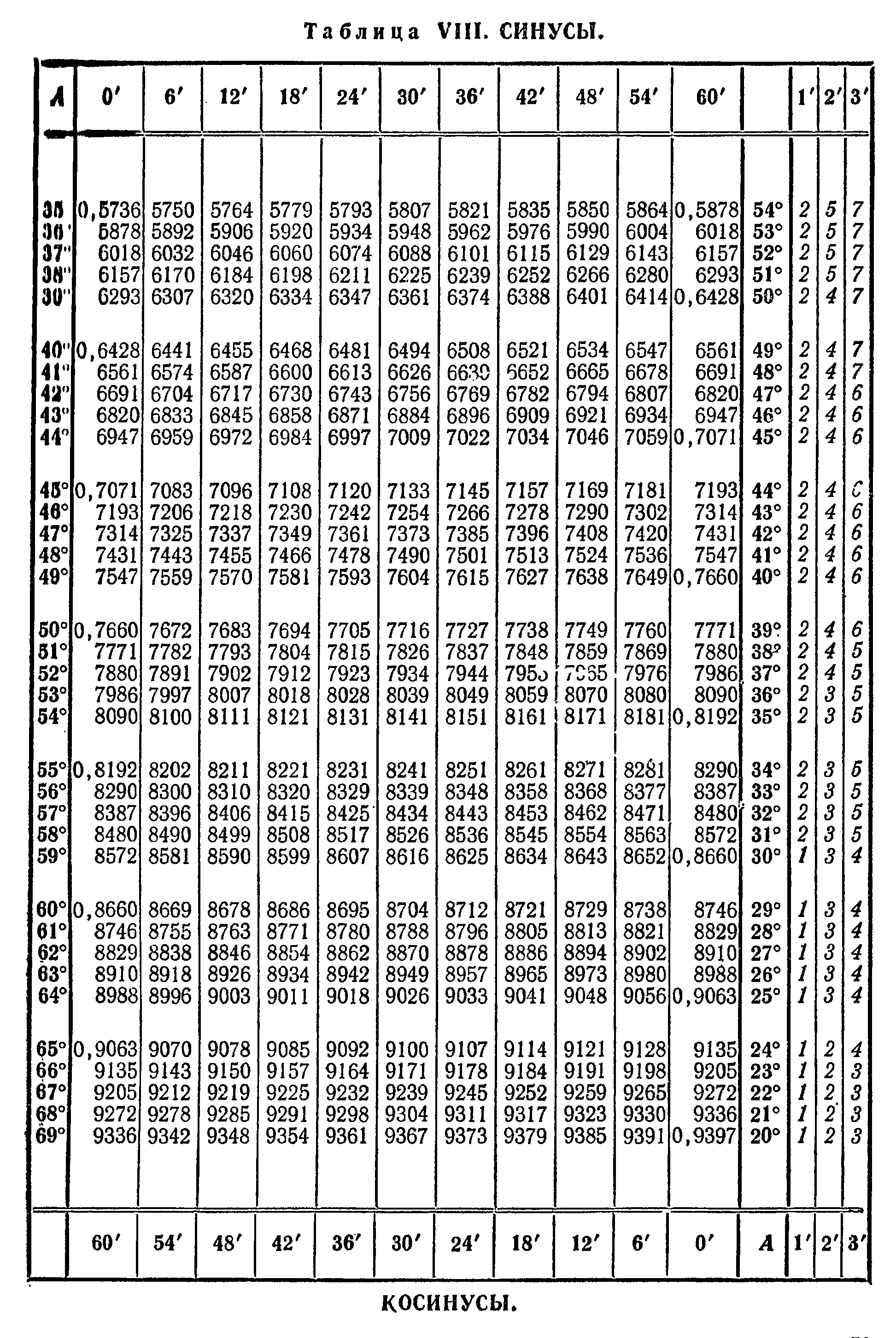
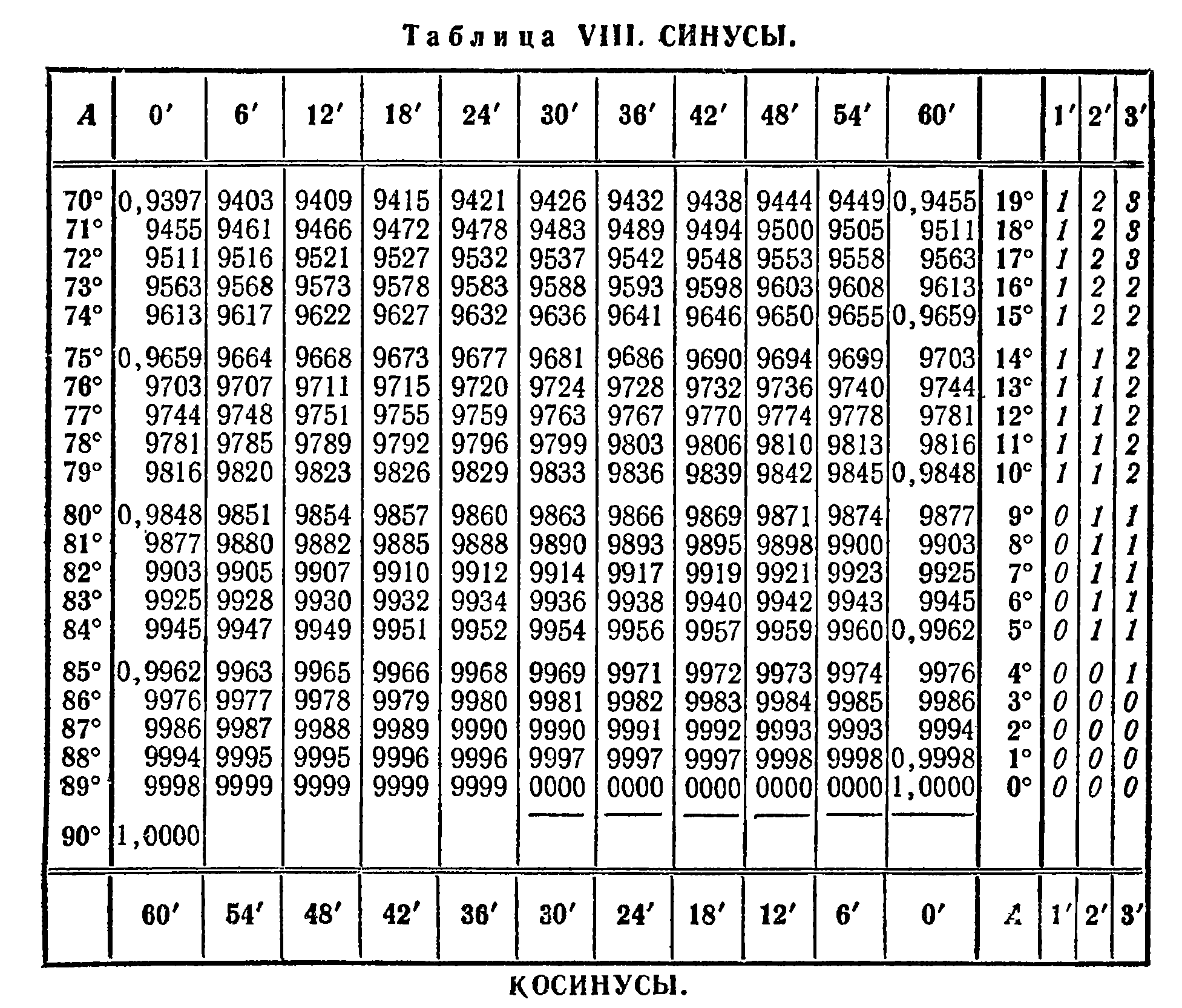
Примеры решения задач

ПРИМЕР 1

Задание	Найти значение синуса $\sin {{43}^{\circ }}$
Решение	Найдем 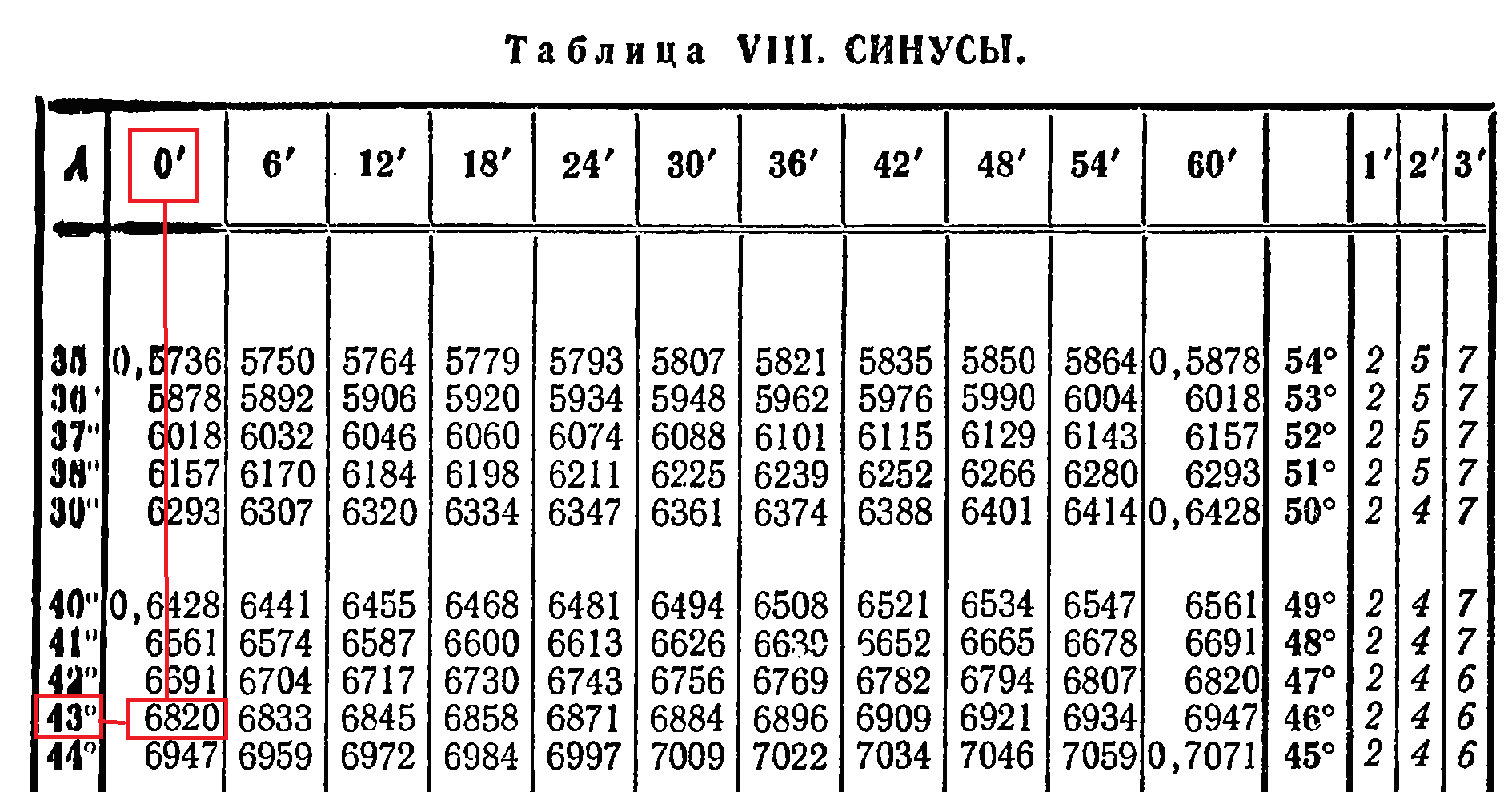$\sin {{43}^{\circ }},$ для этого в первом столбце находим значение ${{43}^{\circ }},$ а в первой строке ${0}'.$ На пересечении ${{43}^{\circ }}$ и ${0}'$ лежит искомое значение 0,6820 (рис. 1) Рис. 1
Ответ	$\sin {{43}^{\circ }}=0,682$

ПРИМЕР 2

Задание	Найти значение синуса $\sin {{5}^{\circ }}2{5}'$
Решение	В первом столбце найдем значение 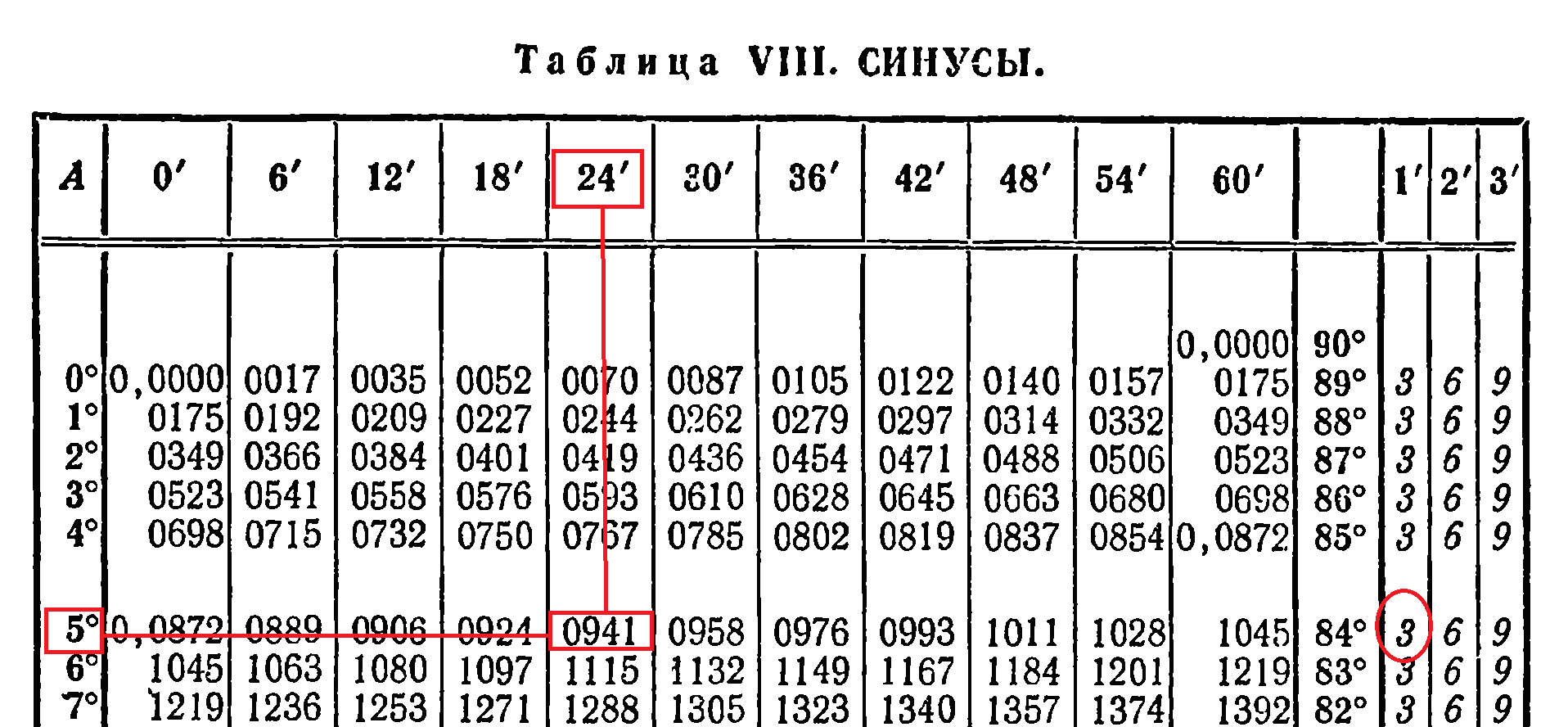${{5}^{\circ }}.$ В первой строке с минутами нет значения $2{5}',$ поэтому выберем ближайшее к этому значение $2{4}'.$ На пересечении соответствующей строки и столбца находится значение $0,0941$ (рис. 2). Это значение $\sin {{5}^{\circ }}2{4}',$ а искомое значение на ${1}'$ больше. В конце строки ${{5}^{\circ }}$ указанно, что ${1}'$ соответствует 3 (рис. 2). Следовательно, чтобы узнать заданное значение синуса необходимо к $0,0941$ прибавить $0,0003,$ получим $\sin {{5}^{\circ }}2{5}'=0,0941+0,0003=0,0944$ Рис. 2
Ответ	$\sin {{5}^{\circ }}2{5}'=0,0944$

ПРИМЕР 3

Задание	Найти значение синуса $\sin {{75}^{\circ }}2{8}'$
Решение	В столбце с градусами найдем 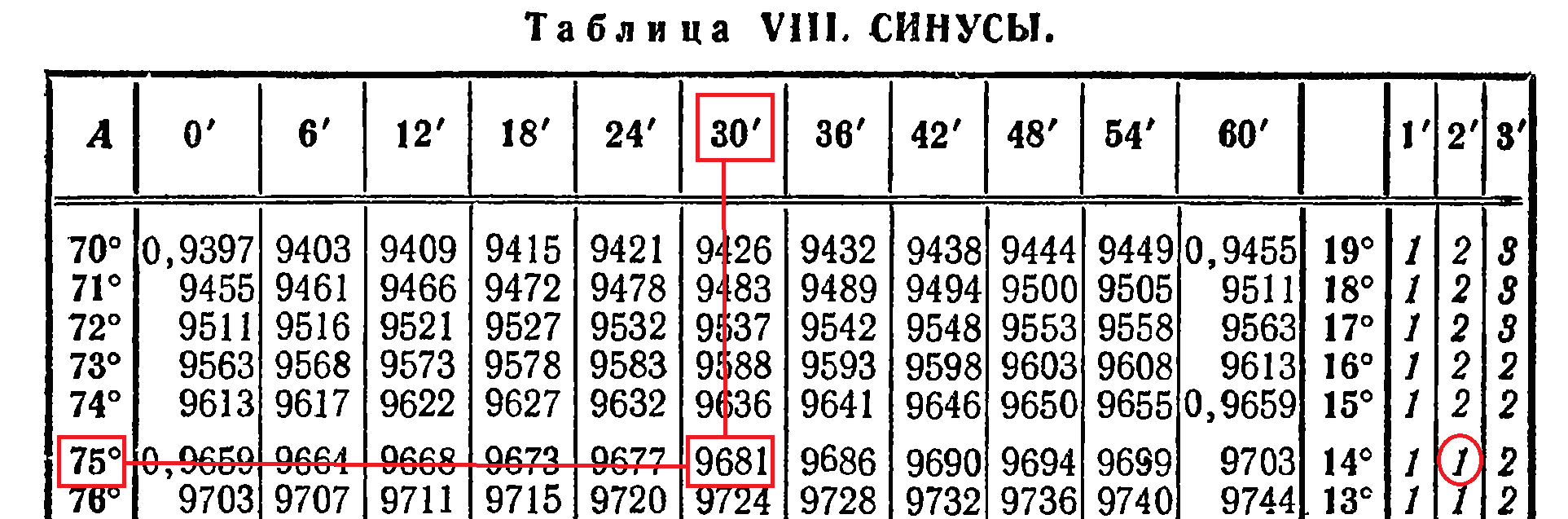${{75}^{\circ }}.$ В строке с минутами нет значения $2{8}',$ поэтому берем ближайшее к этому значение – $3{0}'.$ На пересечении соответствующей строки и столбца находим значение $0,9681$ (рис. 3). Это значение $\sin {{75}^{\circ }}3{0}',$ а искомое значение на ${2}'$ меньше. В конце строки ${{75}^{\circ }}$ указанно, что ${2}'$ соответствует 1 (рис. 3). Следовательно, для определения заданного значения синуса необходимо из $0,9681$ вычесть $0,0001,$ получим $\sin {{5}^{\circ }}2{5}'=0,9681-0,0001=0,9680$ Рис. 3
Ответ	$\sin {{75}^{\circ }}2{8}'=0,968$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Таблица Брадиса (синусы)

Примеры решения задач