Синус двойного угла
![]()
Эту формулу легко получить из формулы синуса суммы
![]()
положив в ней ![]() Действительно
Действительно
![]()
Синус двойного угла еще можно выразить через тангенс и котангенс:
![]()
Примеры решения задач
| Задание | Упростить выражение:
|
| Решение | Выразим первые два множителя через синус двойного угла:
Тогда исходное выражение примет вид Умножим числитель и знаменатель полученного выражения на 2: применим к числителю формулу синуса двойного угла |
| Ответ | 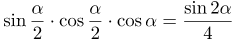 |
| Задание | Найти значение выражения
|
| Решение | Воспользуемся формулой синуса двойного угла |
| Ответ | 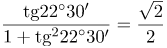 |
| Задание | Упростить выражение
|
| Решение | Распишем в числителе и знаменателе синусы двойного угла, используя формулу Вынесем за скобки в числителе В полученном выражении воспользуемся основным тригонометрическим тождеством и представим единицу как Вынесем в знаменателе Снова в числителе распишем единицу, используя основное тригонометрическое тождество |
| Ответ | 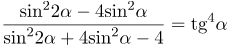 |






![Rendered by QuickLaTeX.com \[\frac{{{\sin }^{2}}2\alpha -4{{\sin }^{2}}\alpha }{{{\sin }^{2}}2\alpha +4{{\sin }^{2}}\alpha -4}=\frac{{{\left( 2\sin \alpha \cdot \cos \alpha \right)}^{2}}-4{{\sin }^{2}}\alpha }{{{\left( 2\sin \alpha \cdot \cos \alpha \right)}^{2}}+4{{\sin }^{2}}\alpha -4}=\frac{4{{\sin }^{2}}\alpha \cdot {{\cos }^{2}}\alpha -4{{\sin }^{2}}\alpha }{4{{\sin }^{2}}\alpha \cdot {{\cos }^{2}}\alpha +4{{\sin }^{2}}\alpha -4}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-bf2ae8fad4553e878bb7ddb04c27e4d5_l3.png)
![Rendered by QuickLaTeX.com \[\frac{{{\sin }^{2}}2\alpha -4{{\sin }^{2}}\alpha }{{{\sin }^{2}}2\alpha +4{{\sin }^{2}}\alpha -4}=\frac{4{{\sin }^{2}}\alpha \left( {{\cos }^{2}}\alpha -1 \right)}{4\left( {{\sin }^{2}}\alpha \cdot {{\cos }^{2}}\alpha +{{\sin }^{2}}\alpha -1 \right)}=\frac{{{\sin }^{2}}\alpha \left( {{\cos }^{2}}\alpha -1 \right)}{\left( {{\sin }^{2}}\alpha \cdot {{\cos }^{2}}\alpha +{{\sin }^{2}}\alpha -1 \right)}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6486fb2bbdff075b8f8d9b46fb341a63_l3.png)
![Rendered by QuickLaTeX.com \[\frac{{{\sin }^{2}}2\alpha -4{{\sin }^{2}}\alpha }{{{\sin }^{2}}2\alpha +4{{\sin }^{2}}\alpha -4}=\frac{{{\sin }^{2}}\alpha \left( {{\cos }^{2}}\alpha -\left( {{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha \right) \right)}{\left( {{\sin }^{2}}\alpha \cdot {{\cos }^{2}}\alpha +{{\sin }^{2}}\alpha -\left( {{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha \right) \right)}= \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-66addd86179bed6a9b20d23159c774d8_l3.png)
![Rendered by QuickLaTeX.com \[=\frac{{{\sin }^{2}}\alpha \left( {{\cos }^{2}}\alpha -{{\sin }^{2}}\alpha -{{\cos }^{2}}\alpha \right)}{\left( {{\sin }^{2}}\alpha \cdot {{\cos }^{2}}\alpha +{{\sin }^{2}}\alpha -{{\sin }^{2}}\alpha -{{\cos }^{2}}\alpha \right)}=\frac{{{\sin }^{2}}\alpha \left( -{{\sin }^{2}}\alpha \right)}{\left( {{\sin }^{2}}\alpha \cdot {{\cos }^{2}}\alpha -{{\cos }^{2}}\alpha \right)}. \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1e180e984c9afbf992a6734488b342aa_l3.png)
![Rendered by QuickLaTeX.com \[\frac{{{\sin }^{2}}2\alpha -4{{\sin }^{2}}\alpha }{{{\sin }^{2}}2\alpha +4{{\sin }^{2}}\alpha -4}=\frac{{{\sin }^{2}}\alpha \left( -{{\sin }^{2}}\alpha \right)}{\left( {{\sin }^{2}}\alpha \cdot {{\cos }^{2}}\alpha -{{\cos }^{2}}\alpha \right)}=\frac{-{{\sin }^{4}}\alpha }{{{\cos }^{2}}\alpha \ \left( {{\sin }^{2}}\alpha -1 \right)}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-15aef3a0011750419d80cfe63ef9f941_l3.png)





