Синус 120 градусов

Значение синуса 120 градусов

ОПРЕДЕЛЕНИЕ

Синус 120 градусов равен $\frac{\sqrt{3}}{2}.$

Действительно 120 градусов можно представить как ${{180}^{\circ }}-{{60}^{\circ }},$ применяя формулы приведения, имеем

$\sin {{120}^{\circ }}=\sin \left( {{180}^{\circ }}-{{60}^{\circ }} \right)=\sin {{60}^{\circ }}=\frac{\sqrt{3}}{2}$

Переведем ${{120}^{\circ }}$ в радианы, составим соответствие

${{360}^{\circ }}-\ 2\pi$

${{120}^{\circ }}-\ x$

По пропорции:

${{360}^{\circ }}=\ 2\pi \cdot {{120}^{\circ }}\quad \Rightarrow x =\ \frac{2\pi \cdot {{120}^{\circ }}}{{{360}^{\circ }}}\quad \Rightarrow \quad x=\ \frac{2\pi }{3}$

Тогда $\sin \ \frac{2\pi }{3}=\frac{\sqrt{3}}{2}.$

На единичной окружности синус 120 градусов находится следующим образом (рис. 1).

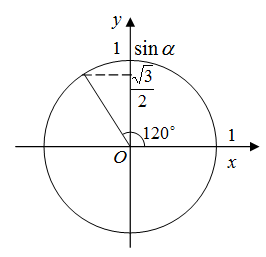
Рис. 1

Примеры решения задач

ПРИМЕР 1

Задание

Найти площадь параллелограмма, если его стороны равны $\sqrt{3}/3$ и 4 см, а один из его углов равен ${{120}^{\circ }}.$

Решение

Площадь параллелограмма можно вычислить по формуле

$S=a\cdot b\cdot \sin \alpha$

где $a$ и $b$ стороны параллелограмма, а $\alpha$ угол между ними. По условию $a=\frac{\sqrt{3}}{3}$ и $b=4,$ а $\alpha ={{120}^{\circ }}.$ Подставляя заданные значения в формулу для площади, получим