Синус 0 градусов
Значение синуса 0 градусов
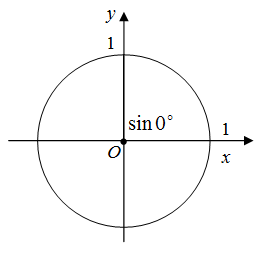
Рис. 1
Примеры решения задач
| Задание | Вычислить модуль векторного произведения сонаправленных векторов, лежащих на одной прямой, с длинами соответственно |
| Решение | Модуль векторного произведения двух векторов равен произведению длин этих векторов на синус угла между ними, то есть
По условию |
| Ответ |
| Задание | Вычислить интеграл
|
| Решение | Домножим числитель и знаменатель подынтегральной функции на 2:
Учитывая, что Далее так как Учитывая, что |
| Ответ | 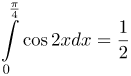 |






![Rendered by QuickLaTeX.com \[ \int\limits_{0}^{\frac{\pi }{4}}{\cos 2xdx} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-37713ab484c2a93d761db4ada0f82a35_l3.png)
![Rendered by QuickLaTeX.com \[\int\limits_{0}^{\frac{\pi }{4}}{\cos 2xdx}=\int\limits_{0}^{\frac{\pi }{4}}{\frac{2\cos 2xdx}{2}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ecd6f3b76e0c867b2299a7128beaf939_l3.png)
![Rendered by QuickLaTeX.com \[\int\limits_{0}^{\frac{\pi }{4}}{\cos 2xdx}=\frac{1}{2}\int\limits_{0}^{\frac{\pi }{4}}{\cos 2xd\left( 2x \right)}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-4098ee43f295c713c9582f9548300429_l3.png)
![Rendered by QuickLaTeX.com \[\int\limits_{0}^{\frac{\pi }{4}}{\cos 2xdx}=\frac{1}{2}\int\limits_{0}^{\frac{\pi }{4}}{\cos 2xd\left( 2x \right)}=\frac{1}{2}\sin 2x\left| \underset{0}{\overset{\frac{\pi }{4}}{\mathop{{}}}}\, \right.=\frac{1}{2}\left( \sin \frac{2\pi }{4}-\sin 0 \right)=\frac{1}{2}\left( \sin \frac{\pi }{2}-\sin 0 \right)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e8c34dec310e8bafc14095f97c61034f_l3.png)
![Rendered by QuickLaTeX.com \[\int\limits_{0}^{\frac{\pi }{4}}{\cos 2xdx}=\frac{1}{2}\left( \sin \frac{\pi }{2}-\sin 0 \right)=\frac{1}{2}\left( 1-0 \right)=\frac{1}{2}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-695a12fad08b4de431f36795ce320825_l3.png)





