Графики тригонометрических функций
Графики синуса и косинуса
График функции ![]() изображен на рисунке 1.
изображен на рисунке 1.
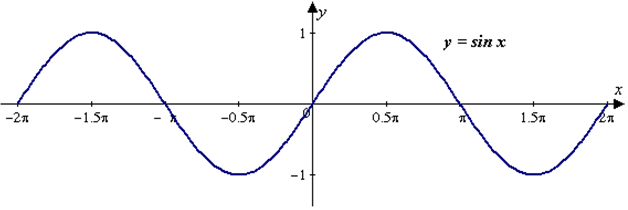
Рис. 1
График функции ![]() изображен на рисунке 2.
изображен на рисунке 2.
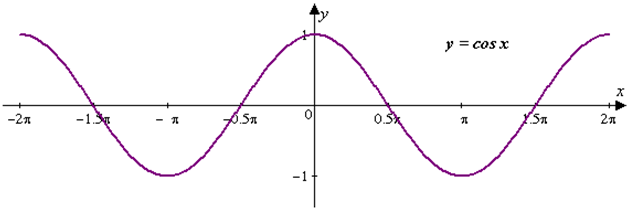
Рис. 2
Кривая, описывающая функцию синуса, называется синусоидой, а косинуса – косинусоидой.
График функции ![]() можно получить из графика функции
можно получить из графика функции ![]() сдвигом последнего влево на
сдвигом последнего влево на ![]() . Аналогично, график функции
. Аналогично, график функции ![]() можно получить из графика функции
можно получить из графика функции ![]() сдвигом последнего вправо на
сдвигом последнего вправо на ![]() .
.
Графики тангенса и котангенса
График функции ![]() изображен на рисунке 3. Кривая, задающая функцию тангенса, называется тангенсоидой.
изображен на рисунке 3. Кривая, задающая функцию тангенса, называется тангенсоидой.
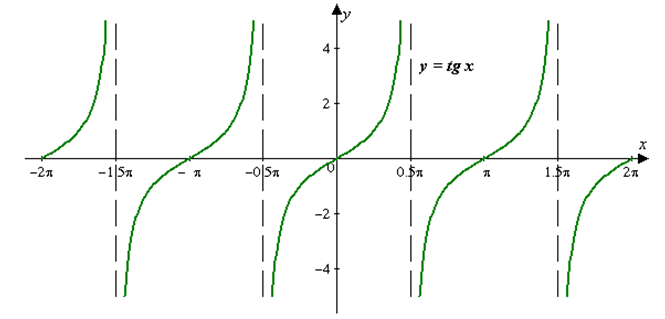
Рис. 3
График функции ![]() изображен на рисунке 4.
изображен на рисунке 4.
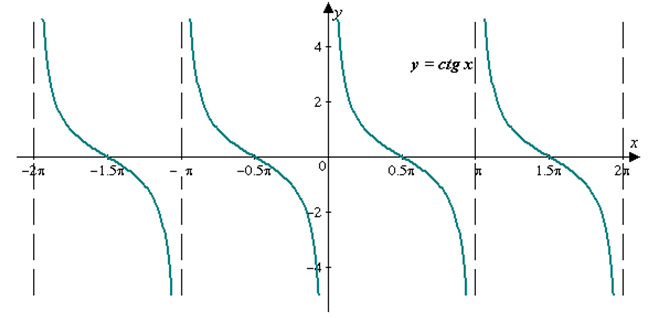
Рис. 4
Примеры решения задач
| Задание | Построить график функции |
| Решение | Искомый график получается из графика функции 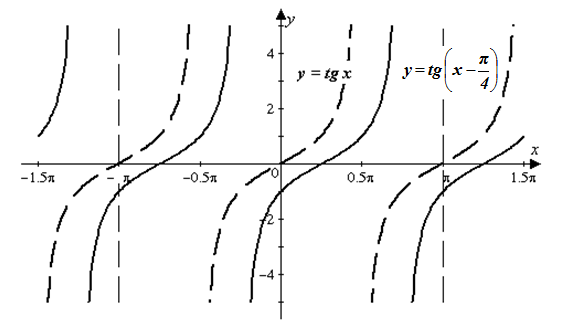
Рис. 5 |
| Задание | Построить график функции |
| Решение | Искомый график получается из графика функции 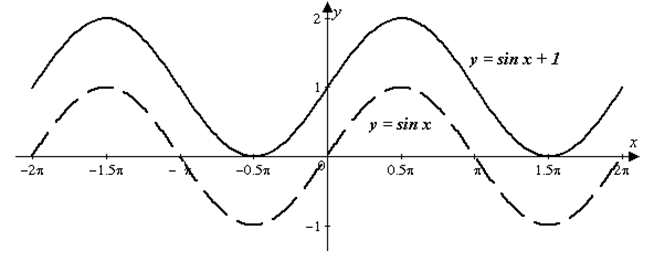
Рис. 6 |
| Задание | Построить график функции |
| Решение | Искомый график получается из графика функции 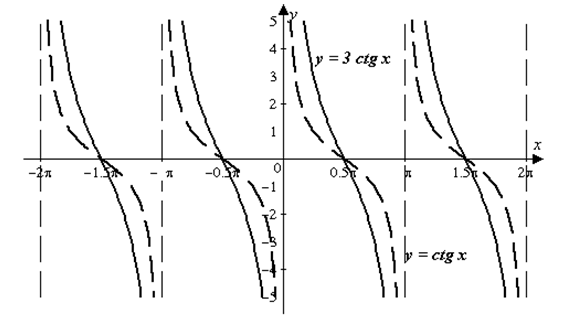
Рис. 7 |
| Задание | Построить график функции |
| Решение | Заданный график построим с помощью элементарных преобразований графика функции 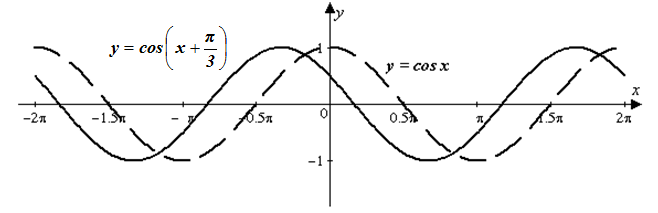
Рис. 8 Затем, отразив график функции 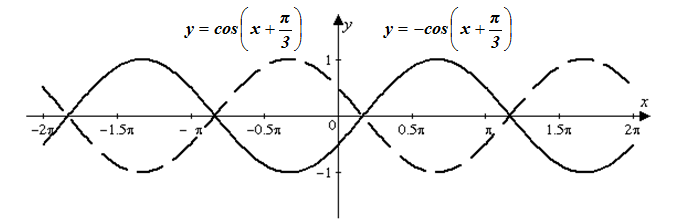
Рис. 9 |











