Синус 90 градусов

Значение синуса 90 градусов

ОПРЕДЕЛЕНИЕ

Синус 90 градусов равен 1, то есть 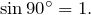$\sin {{90}^{\circ }}=1.$ В радианах 90 градусов это 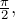$\frac{\pi }{2},$ таким образом 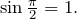$\sin \frac{\pi }{2}=1.$ На тригонометрическом круге синус 90 градусов есть точка пересечения единичной окружности с осью ординат (рис. 1).

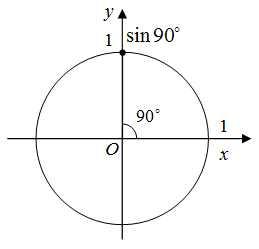
Рис. 1

Примеры решения задач

ПРИМЕР 1

Задание

Вычислить модуль векторного произведения векторов, длины которых равны $\left| {\bar{a}} \right|=2,$ $\left| {\bar{b}} \right|=3,$ а угол между ними ${{90}^{\circ }}.$

Решение

Модуль векторного произведения двух векторов равен произведению длин этих векторов на синус угла между ними, то есть справедлива формула

$\left| \,\left[ \bar{a},\bar{b} \right]\, \right|=\left| {\bar{a}} \right|\cdot \left| {\bar{b}} \right|\cdot \sin \alpha$

По условию $\left| {\bar{a}} \right|=2,$ $\left| {\bar{b}} \right|=3,$ а угол между ними $\alpha ={{90}^{\circ }},$ тогда

$\left| \,\left[ \bar{a},\bar{b} \right]\, \right|=2\cdot 3\cdot \sin {{90}^{\circ }}=2\cdot 3\cdot 1=6$

Ответ

$\left| \,\left[ \bar{a},\bar{b} \right]\, \right|=6$

ПРИМЕР 2

Задание

Доказать, что радиус описанной вокруг прямоугольника треугольника окружности равен половине гипотенузы.

Доказательство

Обозначим гипотенузу произвольного прямоугольного треугольника $c.$ Напомним, что гипотенуза это сторона прямоугольного треугольника, лежащего против прямого угла $\gamma ={{90}^{\circ }}.$ Запишем обобщенную теорему синусов для гипотенузы:

$\frac{c}{\sin \gamma }=2R$

Выразим из этого равенства радиус описанной окружности, учитывая, что $\sin {{90}^{\circ }}=1$

$R=\frac{c}{2\sin {{90}^{\circ }}}\quad \Rightarrow \quad R=\frac{c}{2\cdot 1}\quad \Rightarrow \quad R=\frac{c}{2}$

Что и требовалось доказать.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Синус 90 градусов

Значение синуса 90 градусов

Примеры решения задач