Гиперболический синус

Определение и формулы гиперболического синуса

ОПРЕДЕЛЕНИЕ

Гиперболическим синусом называется функция

$y=\text{sh}x=\frac{{{e}^{x}}-{{e}^{-x}}}{2}, \quad -\infty <x<\infty , -\infty <y<\infty$

Гиперболический синус является нечетной функцией, возрастающей на всей числовой оси. График гиперболического синуса изображен на рисунке 1.

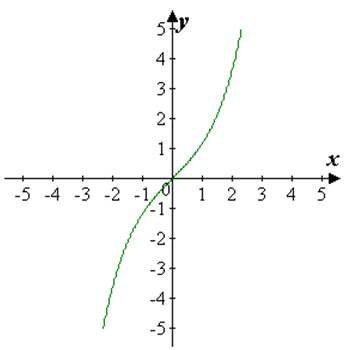
Рис. 1

Гиперболический синус связан с тригонометрическим синусом следующим образом:

$\text{sh}x=-i\sin \left( ix \right)$

$\text{sh}\left( ix \right)=i\sin x$

Гиперболические синус и косинус связаны следующими соотношениями:

$\text{sh}x+\text{ch}x={{e}^{x}}$

$\text{ch}^{2}}x-\text{sh}^{2}}x=1$

Формула для гиперболического синуса суммы и разности аргумента:

$\text{sh}\left( x\pm y \right)=\text{sh}x\cdot \text{ch}y\pm \text{ch}x\cdot \text{sh}y$

Формула гиперболического синуса двойного угла

$\text{sh}2x=2\text{sh}x\cdot \text{ch}x$

Формула произведения гиперболических синусов

$\text{sh}x\cdot \text{sh}y=\frac{\text{ch}\left( x+y \right)-\text{ch}\left( x-y \right)}{2}$

$\text{sh}^{2}}x=\frac{\text{ch}2x-1}{2}$

Формулы суммы и разности гиперболических функций

$\text{sh}x+\text{sh}y=2\text{sh}\frac{x+y}{2}\cdot \text{ch}\frac{x-y}{2}$

$\text{sh}x-\text{sh}y=2\text{sh}\frac{x-y}{2}\cdot \text{ch}\frac{x+y}{2}$

Примеры решения задач

ПРИМЕР 1

Задание

Найти приближенное значение $\text{sh}2$

Решение

По определению $\text{sh}x=\frac{{{e}^{x}}-{{e}^{-x}}}{2},$ подставляем значение $x=2,$ получим

$\text{sh}2=\frac{e^2-e^{-2}}{2}=\frac{1}{2}\left(e^2-\frac{1}{e^2}\right)$

В последнее выражение подставим значение экспоненты $e \approx 2,72$ :

$\text{sh}2\approx \frac{1}{2}\left( {{\left( 2,72 \right)}^{2}}-\frac{1}{{{\left( 2,72 \right)}^{2}}} \right)=\frac{1}{2}\left( 7,3984-\frac{1}{7,3984} \right)\approx \frac{1}{2}\left( 7,3984-0,1352 \right)=3,6316$

Ответ

$\text{sh}2\approx 3,6316$

ПРИМЕР 2

Задание

Доказать тождество $\text{ch}^{2}}x-\text{sh}^{2}}x=1$

Доказательство

По определению

$\text{sh}x=\frac{{{e}^{x}}-{{e}^{-x}}}{2}; \text{ch}x=\frac{{{e}^{x}}+{{e}^{-x}}}{2}$

Подставим эти выражение в левую часть заданного равенства:

$\text{ch}^{2}}x-\text{sh}^{2}}x={{\left( \frac{{{e}^{x}}+{{e}^{-x}}}{2} \right)}^{2}}-\ \,{{\left( \frac{{{e}^{x}}-{{e}^{-x}}}{2} \right)}^{2}}=$

$=\frac{1}{4}\left( {{e}^{2x}}+2{{e}^{x}}\cdot {{e}^{-x}}+{{e}^{-2x}}-\left( {{e}^{2x}}-2{{e}^{x}}\cdot {{e}^{-x}}+{{e}^{-2x}} \right) \right)=$

$=\frac{1}{4}\left( {{e}^{2x}}+2+{{e}^{-2x}}-{{e}^{2x}}+2-{{e}^{-2x}} \right)= \frac{4}{4}=1$

Что и требовалось доказать.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Гиперболический синус

Определение и формулы гиперболического синуса

Примеры решения задач