Произведение синусов
Произведение синусов вычисляется по формуле
![]()
Примеры решения задач
ПРИМЕР 1
| Задание | Преобразовать в сумму произведение: |
| Решение | Воспользуемся формулой для нахождения произведения синусов
получим |
| Ответ | 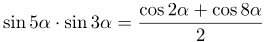 |
ПРИМЕР 2
| Задание | Преобразовать в сумму произведение |
| Решение | По формуле произведения синусов имеем
|
| Ответ | 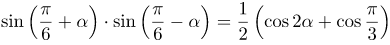 |











