Разность синусов
Разность синусов двух углов равна удвоенному произведению синуса полуразности на косинус полусуммы этих углов, то есть
![]()
Примеры решения задач
ПРИМЕР 1
| Задание | Вычислить:
|
| Решение | Воспользуемся формулой разности синусов:
|
| Ответ | 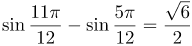 |
ПРИМЕР 2
| Задание | Преобразовать в произведение
|
| Решение | По формуле разности синусов |
| Ответ | 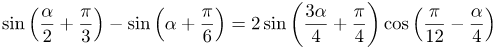 |











