Синус умножить на синус
Эта формула еще называется формулой преобразования произведения синусов в сумму. Можно так же перемножить три синуса, справедлива формула ![]()
Примеры решения задач
ПРИМЕР 1
| Задание | Преобразовать в сумму произведение синусов |
| Решение | Так как произведение синусов равно
|
| Ответ |
ПРИМЕР 2
| Задание | Преобразовать в сумму произведение синусов
|
| Решение | Воспользуемся формулой для произведения трех синусов:
|
| Ответ | 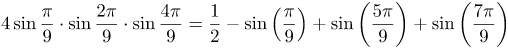 |











