Тригонометрический круг (окружность)

ОПРЕДЕЛЕНИЕ

Тригонометрический круг (окружность) – круг радиуса один (единичная окружность), с центром в начале координат (рисунок 1).

За нулевое положение радиуса, принимается его положение на положительном направлении оси Ox. Угол поворота радиуса отсчитывается от положительного направления оси Ox: с плюсом – против часовой стрелки, с минусом – по часовой стрелке. Полный круг – это ${{360}^{\circ }}$ . Каждому углу $\alpha$ от ${{0}^{\circ }}$ до ${{360}^{\circ }}$ соответствует точка $M$ на единичной окружности.

Синусом угла $\alpha$ есть ордината точки $M$ , а косинусом угла $\alpha$ есть абсцисса точки $M$ .

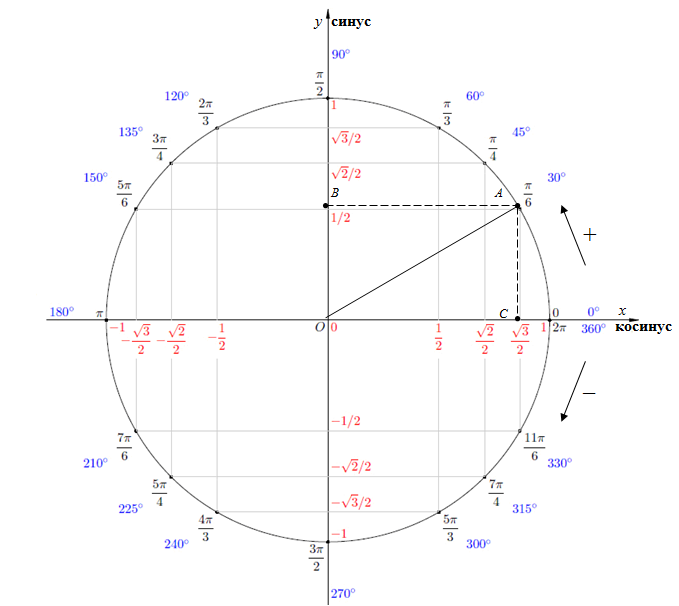
Рис. 1

Примеры решения задач

ПРИМЕР 1

Задание	Используя единичную окружность, определить синус и косинус угла $\frac{\pi }{6}$ .
Решение	Отложим на единичной окружности угол равный $\frac{\pi }{6}$ (рис. 1), ему будет соответствовать точка A окружности. Найдем синус заданного угла. Для этого найдем проекцию точки A на ось Oy, ею будет точка $B\left( 0;\frac{1}{2} \right)$ . Значит, ордината точки A равна $\frac{1}{2}$ и значение $\sin \frac{\pi }{6}=\frac{1}{2}$ . Для нахождения косинуса заданного угла, найдем проекцию точки A на ось Ox. Ею будет точка $C\left( \frac{\sqrt{3}}{2};\ 0 \right)$ , тогда абсцисса точка A равна $\frac{\sqrt{3}}{2}$ и, соответственно, $\cos \frac{\pi }{6}=\frac{\sqrt{3}}{2}$ .
Ответ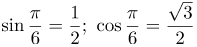

Единицы измерения углов

Углы обычно измеряются либо в градусах, либо в радианах. Перевести градусы в радианы просто: 360 градусов (полный круг) соответствует $2\pi$ радиан.

ПРИМЕР 2

Задание

Перевести:

1) угол $\alpha =\frac{3\pi }{2}$ в градусы;

2) угол $\beta ={{135}^{\circ }}$ в радианы.

Решение

1) Для того чтобы перевести угол из радиан в градусы, умножим данный угол на $\frac{{{360}^{\circ }}}{2\pi }$ . Получим

$\alpha =\frac{3\pi }{2}\cdot \frac{{{360}^{\circ }}}{2\pi }=3\cdot {{90}^{\circ }}={{270}^{\circ }}$

2) Для того чтобы перевести заданный угол из градусов в радианы, умножим его на $\frac{2\pi }{{{360}^{\circ }}}$ . Получим

$\beta ={{135}^{\circ }}\cdot \frac{2\pi }{{{360}^{\circ }}}=\frac{{{270}^{\circ }}\cdot \pi }{{{360}^{\circ }}}=\frac{3\pi }{4}$

Ответ

$1) \alpha ={{270}^{\circ }} \text{ };\text{ } 2)\beta =\frac{3\pi }{4}$

На единичной окружности также можно находить углы, которые больше 360 градусов. Поскольку, значения синуса и косинуса на тригонометрическом круге повторяются каждые ${{360}^{\circ }}$ .

ПРИМЕР 3

Задание

Найти с помощью единичной окружности синус угла $\alpha ={{750}^{\circ }}$ .

Решение

Представим данный угол следующим образом

$\alpha ={{750}^{\circ }}={{360}^{\circ }}+{{360}^{\circ }}+{{30}^{\circ }}$

Таким образом, необходимо сделать два полных обхода окружности, а затем остановиться в точке соответствующей углу в ${{30}^{\circ }}$ (рис. 1). Синусу соответствует ордината этой точки, то есть $\sin {{750}^{\circ }}=\frac{1}{2}$ .

Ответ

$\sin {{750}^{\circ }}=\frac{1}{2}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Тригонометрический круг (окружность)

Примеры решения задач

Единицы измерения углов