Тригонометрические функции числового аргумента
ОПРЕДЕЛЕНИЕ
Тригонометрическими функциями числового аргумента x называются одноименные тригонометрические функции угла равного x радиан.
Например, синусом числового аргумента x называется число равное синусу угла в x радиан. Напомним, что радиан – это угол, соответствующий дуге, длина которой равна ее радиусу.
Примеры решения задач
ПРИМЕР 1
| Задание | Вычислить |
| Решение | Здесь под числом |
| Ответ |
ПРИМЕР 2
| Задание | Вычислить |
| Решение | Согласно определению |
| Ответ | 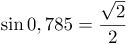 |











