Косинус 120 градусов

Значение косинуса 120 градусов

ОПРЕДЕЛЕНИЕ

Косинус 120 градусов равен $-\frac{1}{2},$ это записывается следующим образом

$\cos {{120}^{\circ }}=-\frac{1}{2}$

Действительно 120 градусов можно представить как ${{180}^{\circ }}-{{60}^{\circ }},$ применяя формулы приведения, имеем:

$\cos {{120}^{\circ }}=\cos \,\left( {{180}^{\circ }}-{{60}^{\circ }} \right)=-\cos {{60}^{\circ }}=-\frac{1}{2}$

В радианах ${{120}^{\circ }},$ составит $\frac{2\pi }{3},$ тогда

$\cos \ \frac{2\pi }{3}=-\frac{1}{2}$

На единичной окружности косинус 120 градусов располагается следующим образом (рис. 1).

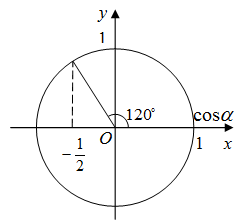
Рис. 1

Примеры решения задач

ПРИМЕР 1

Задание

Найти угол между векторами $\bar{a}$ и $\bar{b},$ если $\left| {\bar{a}} \right|=2, \quad \left| {\bar{b}} \right|=3$ и $\left( \bar{a}+2\,\bar{b} \right)\left( \bar{a}-\,\bar{b} \right)=-17$ .

Решение

Преобразуем выражение $\left( \bar{a}+2\,\bar{b} \right)\left( \bar{a}-\,\bar{b} \right),$ используя свойства скалярного произведения:

$\left( \bar{a}+2\,\bar{b} \right)\left( \bar{a}-\,\bar{b} \right)={{\left| {\bar{a}} \right|}^{2}}+2\,\left( \bar{b},\,\bar{a} \right)-\left( \bar{a},\bar{b} \right)-2\cdot {{\left| \,\bar{b} \right|}^{2}}={{\left| {\bar{a}} \right|}^{2}}+\left( \bar{a},\bar{b} \right)-2\cdot {{\left| \,\bar{b} \right|}^{2}}$

Таким образом, получили равенство

$\left( \bar{a}+2\,\bar{b} \right)\left( \bar{a}-\,\bar{b} \right)={{\left| {\bar{a}} \right|}^{2}}+\left( \bar{a},\bar{b} \right)-2\cdot {{\left| \,\bar{b} \right|}^{2}}$

Подставим в него исходные данные и выразим скалярное произведение $\left( \bar{a},\bar{b} \right)$ :

$-17=4+\left( \bar{a},\bar{b} \right)-18; \quad \Rightarrow \quad \left( \bar{a},\bar{b} \right)=-4+18-17; \quad \Rightarrow \quad \left( \bar{a},\bar{b} \right)=-3$

Из формулы для скалярного произведения

$\left( \bar{a},\,\bar{b} \right)=\left| {\bar{a}} \right|\cdot \left| {\bar{b}} \right|\cos \angle \left( \bar{a},\,\bar{b} \right),$

выразим косинус угла между векторами

$\cos \angle \left( \bar{a},\,\bar{b} \right)=\frac{\left( \bar{a},\,\bar{b} \right)}{\left| {\bar{a}} \right|\cdot \left| {\bar{b}} \right|} \quad \Rightarrow \quad \cos \angle \left( \bar{a},\,\bar{b} \right)=\frac{-3}{2\cdot 3} \quad \Rightarrow \quad \cos \angle \left( \bar{a},\,\bar{b} \right)=-\frac{1}{2} \quad \Rightarrow$

$\Rightarrow \quad \angle \left( \bar{a},\,\bar{b} \right)={{120}^{\circ }}$

Ответ

$\angle \left( \bar{a},\,\bar{b} \right)={{120}^{\circ }}$

ПРИМЕР 2

Задание

Две стороны треугольника относятся как $5:3,$ а угол между ними равен ${{120}^{\circ }}.$ Найдите третью сторону треугольника, если его периметр равен 45 см.

Решение

Сделаем рисунок (рис. 1). Обозначим 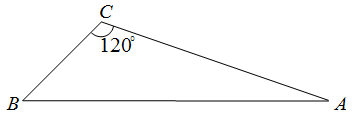$AC=5x, \quad BC=3x,$ тогда искомая сторона $AB.$

Рис. 2

Запишем для стороны AB теорему косинусов:

${{AB}^{2}}={{AC}^{2}}+{{BC}^{2}}-2\cdot AC \cdot BC \cdot \cos {{120}^{\circ }}$

Подставим в это выражение значения сторон и, учитывая, что $\cos {{120}^{\circ }}=-\frac{1}{2},$ получим:

${{AB}^{2}}={{\left( 5x \right)}^{2}}+{{\left( 3x \right)}^{2}}-2\cdot 5x\cdot 3x\cdot \left( -\frac{1}{2} \right);$

${{AB}^{2}}=25{{x}^{2}}+9{{x}^{2}}+15{{x}^{2}}\Rightarrow {{AB}^{2}}=49{{x}^{2}}\Rightarrow AB=7x$

Периметр треугольника равен

$P=AB+AC+BC; \quad \Rightarrow \quad P=7x+5x+3x \quad \Rightarrow \quad P=15x$

По условию $P=45,$ тогда $45=15x \quad \Rightarrow \quad x=3.$ Таким образом искомая сторона равна

$AB=7\cdot 3=21(cm)$

Ответ

$AB=21$ см

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Косинус 120 градусов

Значение косинуса 120 градусов

Примеры решения задач