Косинус 180 градусов

Значение косинуса 180 градусов

ОПРЕДЕЛЕНИЕ

Косинус 180 градусов равен $-1,$ то есть

$\cos {{180}^{\circ }}=-1$

В радианах 180 градусов это $\pi ,$ таким образом

$\cos \,\pi =-1$

На тригонометрическом круге косинус 180 градусов есть точка пересечения единичной окружности с осью ординат (рис. 1).

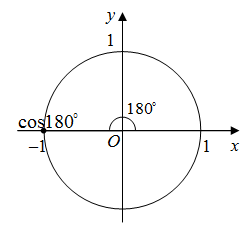
Рис. 1

Примеры решения задач

ПРИМЕР 1

Задание

Доказать, что

$\cos \ \left( {{180}^{\circ }}+\alpha \right)=-\cos \alpha$

Доказательство

Воспользуемся формулой косинуса суммы углов:

$\cos \,\left( \alpha +\beta \right)=\cos \alpha \cdot \cos \beta -\sin \alpha \cdot \sin \beta ;$

$\cos \ \left( {{180}^{\circ }}+\alpha \right)=\cos {{180}^{\circ }}\cdot \cos \alpha -\sin {{180}^{\circ }}\cdot \sin \alpha$

Учитывая, что $\cos {{180}^{\circ }}=-1,$ а $\sin {{180}^{\circ }}=0,$ получим:

$\cos \ \left( {{180}^{\circ }}+\alpha \right)=-1\cdot \cos \alpha -0\cdot \sin \alpha$

или

$\cos \ \left( {{180}^{\circ }}+\alpha \right)=-\cos \alpha$

Что и требовалось доказать.

ПРИМЕР 2

Задание

Найти скалярное произведение двух противоположно направленных векторов $\bar{a}$ и $\bar{b},$ если $\left| {\bar{a}} \right|=5, \quad \left| {\bar{b}} \right|=4.$

Решение

Скалярное произведение двух векторов вычисляется по формуле

$\left( \bar{a},\,\bar{b} \right)=\left| {\bar{a}} \right|\cdot \left| {\bar{b}} \right|\cos \angle \left( \bar{a},\,\bar{b} \right)$

Угол между противоположно направленными векторами составляет ${{180}^{\circ }}.$ Тогда

$\left( \bar{a},\,\bar{b} \right)=5\cdot 4\cdot \cos {{180}^{\circ }}$

Учитывая, что $\cos {{180}^{\circ }}=-1,$ окончательно получим

$\left( \bar{a},\,\bar{b} \right)=5\cdot 4\cdot \left( -1 \right)=-20$

Ответ

$\left( \bar{a},\,\bar{b} \right)=-20$

Понравился сайт? Расскажи друзьям!