Косинус 60 градусов

Значение косинуса 60 градусов

ОПРЕДЕЛЕНИЕ

Косинус 60 градусов равен $\frac{1}{2},$ это записывается следующим образом

$\cos \,\,{{60}^{\circ }}=\frac{1}{2}$

В радианах ${{60}^{\circ }}$ это $\frac{\pi }{3},$ тогда можно так же записать

$\cos \ \,\frac{\pi }{3}=\frac{1}{2}$

Так как косинусу на единичной окружности соответствует ось абсцисс, то косинус 60 градусов на ней выглядит следующим образом (рис. 1).

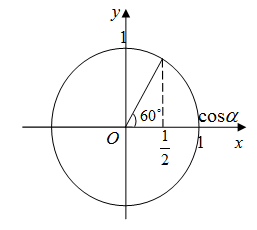
Рис. 1

Примеры решения задач

ПРИМЕР 1

Задание

Две стороны треугольника равны 6 дм и 8 дм, а угол между ними – ${{60}^{\circ }}.$ Найдите третью сторону треугольника.

Решение

Введем обозначения: пусть искомая сторона $a,$ сторона $b=6$ дм, а сторона $c=8$ дм, угол между ними $\alpha ={{60}^{\circ }}.$ По теореме косинусов

${{a}^{2}}={{b}^{2}}+{{c}^{2}}-2\cdot b\cdot c\cdot \cos \alpha$

Подставим в последнее равенство заданные значения сторон и угла:

${{a}^{2}}={{6}^{2}}+{{8}^{2}}-2\cdot 6\cdot 8\cdot \cos {{60}^{\circ }}$

Учитывая, что $\cos \,\,{{60}^{\circ }}=\frac{1}{2},$ получим

${{a}^{2}}=36+64-2\cdot 6\cdot 8\cdot \frac{1}{2}\ \quad \Rightarrow \ \quad {{a}^{2}}=52\ \quad \Rightarrow \ \quad a=2\sqrt{13} (dm)$

Ответ

$a=2\sqrt{13}$ дм

ПРИМЕР 2

Задание

Основания прямоугольной трапеции равны 12 см и 18 см, а острый угол трапеции – ${{60}^{\circ }}.$ Найти большую боковую сторону трапеции.

Решение

Сделаем рисунок (рис. 2).

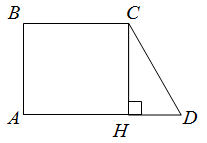
Рис. 2

Обозначим $BC=12$ см; $AD=18$ см; $\angle D={{60}^{\circ }}.$ Проведем в прямоугольной трапеции $ABCD$ высоту $CH$ к большему основанию. Тогда $AH=BC,$ а $AD=AH+HD.$

Отсюда

$HD=AD-AH; \quad \Rightarrow \quad HD=AD-BC$

Подставляя в последнее равенство заданные сторон оснований трапеции, получим

$HD=18-12=6 dm$

Далее рассмотрим прямоугольный треугольник $\Delta CHD, \quad \angle H={{90}^{\circ }}.$ По определению косинус есть отношение прилежащего катета к гипотенузы. Тогда

$\cos \angle D=\frac{HD}{CD}\ \quad \Rightarrow \ \quad CD=\frac{HD}{\cos \angle D}\ \quad \Rightarrow \ \quad CD=\frac{6}{\cos \ {{60}^{\circ }}}$

учитывая, что $\cos \,\,{{60}^{\circ }}=\frac{1}{2},$ окончательно получим

$CD=6\div \frac{1}{2}\ \quad \Rightarrow \ \quad CD=12 (cm)$

Ответ

$CD=12$ см

Понравился сайт? Расскажи друзьям!