Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Тригонометрия Косинус 90 градусов

Косинус 90 градусов

Значение косинуса 90 градусов

ОПРЕДЕЛЕНИЕ

Косинус 90 градусов равен 0, то есть

$\cos {{90}^{\circ }}=0$

В радианах 90 градусов это $\frac{\pi }{2},$ таким образом,

$\cos \frac{\pi }{2}=0$

На тригонометрическом круге косинус 90 градусов есть точка пересечения единичной окружности с осью ординат (рис. 1).

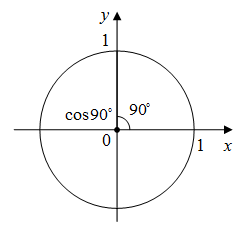
Рис. 1

Примеры решения задач

ПРИМЕР 1

Задание

Доказать, что скалярное произведение ортогональных векторов равно 0.

Доказательство

Пусть $\bar{a}$ и $\bar{b}$ ортогональные вектора, то есть угол между ними $\angle \left( \bar{a},\,\bar{b} \right)={{90}^{\circ }}.$ Скалярное произведение двух векторов вычисляется по формуле:

$\left( \bar{a},\,\bar{b} \right)=\left| {\bar{a}} \right|\cdot \left| {\bar{b}} \right|\cos \angle \left( \bar{a},\,\bar{b} \right)$

Тогда

$\left( \bar{a},\,\bar{b} \right)=\left| {\bar{a}} \right|\cdot \left| {\bar{b}} \right|\cos {{90}^{\circ }}$

Так как $\cos {{90}^{\circ }}=0,$ то $\left( \bar{a},\,\bar{b} \right)=\left| {\bar{a}} \right|\cdot \left| {\bar{b}} \right|\cdot 0\ \quad \Rightarrow \ \quad \left( \bar{a},\,\bar{b} \right)=0.$

Что и требовалось доказать.

ПРИМЕР 2

Задание

Доказать, что $\cos \,\left( {{90}^{\circ }}-\alpha \right)=\sin \alpha$

Доказательство

Воспользуемся формулой косинуса разности углов

$\cos \,\left( \alpha -\beta \right)=\cos \alpha \cdot \cos \beta +\sin \alpha \cdot \sin \beta$

Тогда

$\cos \,\left( {{90}^{\circ }}-\alpha \right)=\cos {{90}^{\circ }}\cdot \cos \alpha +\sin {{90}^{\circ }}\cdot \sin \alpha ;$

учитывая, что $\cos {{90}^{\circ }}=0$ и $\sin {{90}^{\circ }}=1,$ получим

$\cos \,\left( {{90}^{\circ }}-\alpha \right)=0\cdot \cos \alpha +1\cdot \sin \alpha ;$

$\cos \,\left( {{90}^{\circ }}-\alpha \right)=\sin \alpha$

Что и требовалось доказать.

Читайте также:

Косинус 120 градусов

Косинус 180 градусов

Косинус двойного угла

График косинуса

Разность косинусов

Косинус суммы

Формулы синусов и косинусов

Косинус угла

© SolverBook - онлайн сервисы для учебы, 2015

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Почта для связи: info@ru.solverbook.com

Выберите язык:

Сервисы

SolverBook