Уравнение Лапласа

Определение и формула уравнения Лапласа

ОПРЕДЕЛЕНИЕ

Дифференциальное уравнение в частных производных вида:

$\Delta =\frac{{\partial }^2f}{\partial x^2}+\frac{{\partial }^2f}{\partial y^2}+\frac{{\partial }^2f}{\partial z^2}=0 \qquad (1)$

называется уравнением Лапласа в декартовых координатах.

Оно является частным случаем уравнения Гельмгольца. Может рассматриваться в трехмерном (1), двумерном (2), одномерном и n – мерном пространствах:

$\frac{{\partial }^2f}{\partial x^2}+\frac{{\partial }^2f}{\partial y^2}=0 \qquad (2)$

$\frac{d^2f}{dx^2}=0 \qquad (3)$

$\Delta f=0 \qquad (4)$

Оператор $\Delta =\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}+\frac{{\partial }^2}{\partial z^2}+\dots$ называется оператором Лапласа (Оператор Лапласа эквивалентен последовательному взятию операций градиента и дивергенции.).

Решение уравнения Лапласа

Решениями уравнения Лапласа являются гармонические функции.

Уравнение Лапласа относится к эллиптическим уравнениям. Неоднородное уравнение Лапласа становится уравнением Пуассона.

Каждое решение уравнения Лапласа в ограниченной области G однозначно выделяется краевыми условиями, накладываемыми на поведение решения (или его производных) на границе $\partial G$ области G. Если решение отыскивается во всём пространстве $R^n$ , краевые условия сводятся к предписанию некоторой асимптотики для f при $x_1, \dots , x_n$ . Задача о нахождении таких решений называется краевой задачей. Чаще всего встречаются задача Дирихле, когда на границе задано значение самой функции f, и задача Немана, когда задано значение производной f по нормали к границе.

Уравнение Лапласа в сферических, полярных и цилиндрических координатах

Уравнение Лапласа можно записать не только в декартовых координатах.

В сферических координатах ( $r,\varphi ,\theta )$ уравнение Лапласа имеет следующий вид:

$\frac{1}{r^2}\cdot \frac{\partial }{\partial r}\left(r^2\frac{\partial f}{\partial r}\right)+\frac{1}{r^2\sin\theta \partial\theta }\left(\sin\theta \cdot \frac{\partial f}{\partial \theta }\right)+\frac{{\partial }^2f}{r^2{\sin}^2\theta \partial{\varphi }^2}=0 \qquad (5)$

В полярных координатах ( $r,\varphi )$ система координат уравнение имеет вид:

$\frac{1}{r}\cdot \frac{\partial }{\partial r}\left(r\frac{\partial f}{\partial r}\right)+\frac{{\partial }^2f}{r^2\partial {\varphi }^2}=0 \qquad \qquad (6)$

В цилиндрических координатах ( $r,\varphi ,z)$ уравнение имеет вид:

$\frac{1}{r}\cdot \frac{\partial }{\partial r}\left(r\frac{\partial f}{\partial r}\right)+\frac{{\partial }^2f}{\partial z^2}+\frac{{\partial }^2f}{r^2\partial {\varphi }^2}=0 \qquad \qquad (7)$

К уравнению Лапласа приводят многие задачи физики и механики, в которых физическая величина является функцией только координат точки. Так, уравнение Лапласа описывает потенциал сил тяготения в области, не содержащей тяготеющих масс, потенциал электростатического поля – в области, не содержащей зарядов, температуру при стационарных процессах и т. д. Большое количество инженерных задач, связанных, в частности, с медленным стационарным обтеканием корпуса корабля, стационарной фильтрацией подземных вод, возникновением поля вокруг электромагнита, а также стационарного электрического поля в окрестности фарфорового изолятора или заглубленного в землю электрического кабеля переменного поперечного сечения, сводится к решению трехмерных уравнений Лапласа или Пуассона. Большое значение оператор Лапласа играет в квантовой механике.

Примеры решения задач

ПРИМЕР 1

Задание

Найдите поле между двумя коаксиальными цилиндрами с радиусами 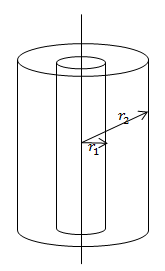$r_1$ и $r_2$ , разность потенциалов между которыми равна $\Delta U.$

рис. 1.

Решение

Запишем уравнение Лапласа в цилиндрических координатах с учетом аксиальной симметрии:

$\frac{1}{r}\cdot \frac{\partial }{\partial r}\left(r\frac{\partial \varphi }{\partial r}\right)=0\qquad (1.1)$

Оно имеет решение $\varphi =-A \text{ln} (r)$ +B. Выберем нулевой потенциал на наружном цилиндре, найдем, получим:

$\varphi \left(r_2\right)=0=-A \text{ln} r_2+B,$ следовательно

$B=A \text{ln} r_2$

$\varphi \left(r_1\right)=\Delta U=-A \text{ln} r_1+B$ , получим:

$A=\frac{\Delta U}{{\ \text{ln} \left(\frac{r_2}{r_1}\right)\ }}$

В результате имеем: $\varphi (r)=-\frac{\Delta U}{{ \text{ln} \left(\frac{r_2}{r_1}\right)\ }} \text{ln} \left(r\right)+\frac{\Delta U}{{ \text{ln} \left(\frac{r_2}{r_1}\right)\ }} \text{ln} r_2$

Ответ

Поле между двумя коаксиальными цилиндрами задается функцией

$\varphi (r)=-\frac{\Delta U}{{ \text{ln} \left(\frac{r_2}{r_1}\right)\ }} \text{ln} \left(r\right)+\frac{\Delta U}{{ \text{ln} \left(\frac{r_2}{r_1}\right)\ }} \text{ln} r_2$

ПРИМЕР 2

Задание

Исследовать устойчивость равновесия положительно заряженной частицы в электрическом поле (теорема Ирншоу).

Решение

Поместим начало координат в положение равновесия частицы. При этом можно считать, что потенциал представляется в виде:

$\varphi \left(x,y,z\right)\approx \frac{1}{2}\left(\frac{{\partial }^2\varphi }{\partial x^2}x^2+\frac{{\partial }^2\varphi }{\partial y^2}y^2+\frac{{\partial }^2\varphi }{\partial z^2}z^2\right)$

где все производные берутся в точке равновесия. Для устойчивости положительного заряда, необходимо, чтобы потенциальная энергия возрастала по любому из направлений, т.е. вторые производные от $\varphi$ по координатам были больше 0 ( $\frac{{\partial }^2\varphi }{\partial x^2}>0,\ \frac{\partial^2 \varphi}{\partial y^2}>0,\ \frac{\partial^2 \varphi}{\partial z^2}>0).$ Но это противоречит уравнению Лапласа $\Delta \varphi =0.$ Если $\frac{{\partial }^2\varphi }{\partial x^2}=\ \frac{{\partial }^2\varphi }{\partial y^2}=\ \frac{{\partial }^2\varphi }{\partial z^2}=0,$ нужно учесть следующие члены разложения $\varphi .$ Можно показать, что и в этом случае устойчивое равновесие невозможно.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Уравнение Лапласа

Определение и формула уравнения Лапласа

Решение уравнения Лапласа

Уравнение Лапласа в сферических, полярных и цилиндрических координатах

Примеры решения задач