Уравнение неразрывности потока

ОПРЕДЕЛЕНИЕ

Уравнение неразрывности является фундаментальным для физики. Это уравнение – математическое выражение закона сохранения. Применяется оно в различных разделах физики. В частности, широко используется для гидроаэромеханики, электромеханике. Так, в процессе движения жидкости должен выполняться закон сохранения массы. Математическим выражением этого закона в гидромеханике и служит уравнение неразрывности.

Основные формы записи уравнения неразрывности потока жидкости

В переменных Эйлера оно может быть записано в нескольких эквивалентных формах:

$\frac{d\rho }{dt}+\rho div\overrightarrow{v}=0,$ или $\frac{d\rho }{dt}+\rho \left(\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial x}+\frac{\partial v_z}{\partial x}\right)=0\qquad (1)$

где $\rho (x,y,z,t)$ — плотность жидкости, $\overrightarrow{v}$ — ее скорость движения.

Следующая распространенная форма записи уравнения неразрывности:

$\frac{d\rho }{dt}+div\left(\rho \overrightarrow{v}\right)=0$ , или $\frac{d\rho }{dt}+\frac{\partial \left(\rho v_x\right)}{\partial x}+\frac{\partial {(\rho v}_y)}{\partial x}+\frac{\partial (\rho v_z)}{\partial x}=0\ \qquad (2)$

И третья форма записи:

$\frac{d\rho }{dt}+\rho div\overrightarrow{v}+\overrightarrow{v}grad\rho =0,$ или $\frac{d\rho }{dt}+\rho \left(\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial x}+\frac{\partial v_z}{\partial x}\right)+\left(v_x\frac{\partial \rho }{\partial x}+v_x\frac{\partial \rho }{\partial x}+v_z\frac{\partial \rho }{\partial x}\right)=0 \qquad \qquad (3)$

Уравнение неразрывности для несжимаемой жидкости ( $\frac{d\rho }{dt}=0)$ будет иметь вид:

$div\overrightarrow{v}=0(4),$ или $\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial x}+\frac{\partial v_z}{\partial x}=0\ (5)\$

Величина и направление скорости в рассматриваемых точках пространства в потоке жидкости могут меняться со временем. Если ни в одной из точек потока вектор скорости $\overrightarrow{v}$ с течением времени не изменяется, то течение жидкости называется установившимся или стационарным. Тогда уравнение неразрывности для стационарного движения несжимаемой жидкости записывают в виде:

$div\left(\rho \ \overrightarrow{v}\right)=0,$ или $\frac{\partial \left(\rho v_x\right)}{\partial x}+\frac{\partial {(\rho v}_y)}{\partial x}+\frac{\partial (\rho v_z)}{\partial x}=0\ \qquad \qquad (6)$

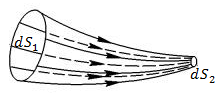
рис. 1

Из уравнения (6) легко получить условие, которое называется условием течения потока жидкости в элементарной струйке или уравнением неразрывности струи, а именно:

${\rho }_1v_1dS_1={\rho }_2v_2dS_{2\ } \qquad \qquad (7)$

где $dS_1$ и $dS_2$ – поперечные сечения элементарной струйки.

Это выражение означает, что при установившемся течении поток жидкости сквозь поперечное сечение струйки не зависит от места положения этого сечения.

Примеры решения задач

ПРИМЕР 1

Задание

На поршень шприца площади 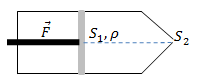$S_1$ действует сила F. С какой скоростью v должна вытекать в горизонтальном направлении струя из отверстия иглы площади $S_2$ ? Плотность жидкости $\rho$ . Трением пренебречь.

рис. 2

Решение

Запишем уравнение неразрывности для струйки:

$S_1l_1=S_2l_2,\qquad (1.1)$

так как жидкость из шприца вытекает вся, то

$l_1=v_1t,\ l_2=v_2t$

где $v_2$ – скорость истечения струи.

Если считать жидкость идеальной, то можно использовать уравнение Бернулли:

$p+\rho gh+\frac{\rho v^2}{2}=const\qquad (1.2)$

Используем условия задачи, например, то, что h не изменяется, перепишем уравнение Бернулли для 2 состояний, учтем, что:

$p=\frac{F}{S_1}$

$\frac{F}{S_1}+p_0+\frac{\rho v^2_1}{2}=p_0+\frac{\rho v^2_2}{2}\qquad (1.3.)$

где $p_0$ — атмосферное давление.

Из уравнения неразрывности:

$S_1v_1=S_2v_2$ отсюда $v_1=\frac{S_2v_2}{S_1},\qquad (1.4.)$

подставим 1.4 в 1.3, получим:

$\frac{F}{S_1}+\frac{\rho S^2_2v^2_2}{2S^2_1}=\frac{1}{2}\rho v^2_2$

отсюда $v_2=\sqrt{\frac{2FS_1}{\rho (S^2_1-S^2_2)}}$ .

Ответ

Скорость истечения жидкости из отверстия $v=\sqrt{\frac{2FS_1}{\rho (S^2_1-S^2_2)}}$

ПРИМЕР 2

Задание

Рассмотрим вертикальный поток жидкости рис. 3. На расстоянии h диаметр струи изменяется от $d_{1\ }$ до $d_{2\ }$ . Сколько воды вытечет за время t? Считать течение жидкости стационарным.