Уравнение движения тела

В том случае, если мы имеем дело с твердым телом, которое в общем случае имеет 6 степеней свободы, то общая система уравнений движения должна содержать шесть независимых уравнений. Их можно представить в виде производных по времени от двух векторов: импульса и момента импульса тела.

Общие законы и уравнения движения системы тел

Произвольную систему тел всегда можно свести к системе материальных точек. Это видно из того, что отдельное тело конечных размеров всегда мысленно можно разбить на столь малые части (частицы), что каждую часть можно рассматривать как материальную точку. Таким образом, выясняя общие законы движения системы тел, можно исходить из представления о системе материальных точек. Соответственно, имеем первое уравнение:

$\frac{d\overline{p}}{dt}=\overline{F}\ (1)$

где $\overline{p}$ — полный импульс тела, $\overline{F}$ – результирующая внешних сил, действующих на тело.

В случае поступательного движения твердого тела его скорость $\overline{v}$ скорости центра масс этого тела: $\overline{v}=\overline{v_c}$ . Соответственно, основное уравнение динамики поступательного движения твердого тела имеет вид:

$\frac{d}{dt}\left(m\overline{v}\right)={\overline{F}}^{vnesh}(2)$

или

$\overline{a}=\frac{{\overline{F}}^{vnesh}}{m}$

где $m$ — масса тела, $\overline{a}$ — его ускорение.

Второе уравнение движения записывается для тела вращающегося относительно неподвижной точки (полюса), и имеет вид:

$\frac{d\overline{L}}{dt}={\overline{M}}^{vnesh}\ \left(3\right)$

где $\overline{L}$ — момент импульса, ${\overline{M}}^{vnesh}$ — момент внешних сил, приложенных к телу.

Уравнение движения твердого тела

Уравнение динамики твердого тела, вращающегося вокруг неподвижной точки О, в жестко связанной с телом подвижной системе координат (x’,y’,z’), начало которой находится в точке О, имеет вид:

$\frac{\hat{d}\overline{L}}{dt}={\overline{M}}^{vnesh}-\overline{w}\times \overline{L\ }\left(4\right)$

где $\overline{w}$ — угловая скорость вращения тела, а $\frac{\hat{d}\overline{L}}{dt}=\frac{dL_{x'}}{dt}\overline{i'}+\frac{dL_{y'}}{dt}\overline{j'}+\frac{dL_{z'}}{dt}\overline{k'}$ — относительная производная по времени от вектора $\overline{L},\ \overline{i'},\overline{j'},\ \overline{k'}$ — орты подвижной системы.

Если оси подвижной системы координат совпадают с главными осями инерции тела в точке О, то уравнения движения тела в проекциях на эти оси имеют вид:

$J_1\dot{w_1}+(J_3-J_2)w_2w_3=M_1,$

$J_2\dot{w_2}+(J_1-J_3)w_1w_3=M_2,\ \ (5)$

$J_3\dot{w_3}+(J_2-J_1)w_1w_2=M_3,$

где $J_1,\ J_2,\ J_3$ – главные моменты инерции тела в точке О, $w_1,\ w_2,\ w_3$ – проекции вектора угловой скорости тела на главные оси инерции, $\dot{w}=\frac{dw}{dt},\ M_1,\ M_2,\ M_3$ – моменты внешних сил относительно тех же осей. Эти уравнения называют динамическими уравнениями Эйлера.

Уравнение движения тела, вращающегося вокруг неподвижной оси

Уравнение движения тела, вращающегося вокруг неподвижной оси (например, оси Оz):

$\frac{dL_z}{dt}={M_z}^{vnesh}\ \left(6\right)$

или

$\frac{d}{dt}\left(J_zw_z\right)={M_z}^{vnesh}$

где $J_z$ – момент инерции тела относительно оси Oz. Если тело не деформируется, то $J_z$ — постоянная, тогда уравнение движения:

$J_z{\varepsilon }_z={M_z}^{vnesh}\ \left(7\right)$

где ${\varepsilon }_z=\frac{dw}{dt}$ – угловое ускорение тела.

Свободное твердое тело в общем случае участвует одновременно в двух движениях- поступательном со скоростью $\overline{v_c}$ центра масс и вращательном вокруг центра масс с угловой скоростью $\overline{w}$ . Векторы $\overline{v_c}$ и $\overline{w}$ удовлетворяют двум дифференциальным уравнениям движения свободного тела (которые получают из 2 и 3), подстановкой соответствующих скоростей центра масс:

$\frac{d}{dt}\left(m\overline{v_c}\right)={\overline{F}}^{vnesh}\ (8)$

$\frac{d\overline{L'_c}}{dt}={\overline{M}}^{vnesh}_c\ (9)$

где m- масса тела, $\overline{v_c}$ — скорость центра масс, ${\overline{F}}^{vnesh}$ — вектор результирующей внешней силы, ${\overline{M}}^{vnesh}_c$ — вектор результирующий моментов внешних сил относительно центра масс C, $\overline{L'_c}=\int_m{\overline{r'}\times \overline{v'}dm}$ , где $\overline{r'},\ \overline{v'}$ — радиус вектор и скорость малого элемента массой dm в поступательно движущейся системе координат с началом в точке C.

Примеры решения задач

ПРИМЕР 1

Задание

Тело брошено под углом $\alpha$ к горизонту с начальной скоростью $\overline{v_0}$ . Напишите уравнение траектории движения тела.

Решение

Сделаем рисунок

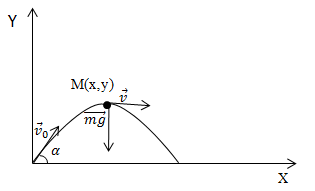
рис. 1

Тело движется под действием постоянной силы тяжести $\overline{mg}$ , которая направлена вертикально вниз (рис. 1). Для произвольной точки M(x,y) имеем:

$\frac{d}{dt}\left(m\overline{v}\right)={\overline{F}}^{vnesh}=const=\overline{mg}$

, следовательно $m\overline{v}=\overline{mg}+m{\overline{v}}_0$ , или $\overline{v}=\overline{g}+{\overline{v}}_0\ (1.1)$ .

Запишем проекции на оси Ox и Oy уравнения (1.1):

$v_x=v_0\cos\alpha ,\ \ v_y=v_0\sin\alpha -gt\ (1.2)$

Проинтегрируем (1.2) по времени, При интегрировании учтем, что начало координат мы поместили в точку бросания, соответственно $x(0)=0, y(0)=0$ , получим:

$x=v_0t\ \cos\alpha ,\ y=v_0t\ \sin\alpha -\frac{gt^2}{2}$

Выразим время из x подставим в y получим уравнение траектории движения тела:

$y=x\text{tg}\alpha -\frac{gx^2}{2v^2_0\cos^2\alpha }$

Ответ

Уравнение траектории движения тела при заданных условиях: $y=x\text{tg}\alpha -\frac{gx^2}{2v^2_0\cos^2\alpha }$

ПРИМЕР 2

Задание

На рисунке дан график угловой скорости твердого тела вращающегося вокруг оси (рис. 2). Укажите точку на графике, соответствующую нулевому значению момента сил, приложенных к телу.

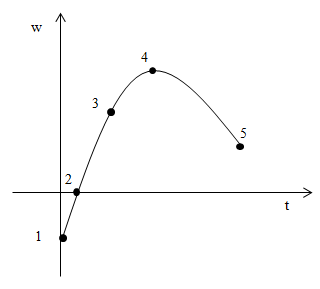
рис. 2

Решение

Запишем уравнение движения для вращающегося тела:

$\frac{d}{dt}\left(J_zw_z\right)={M_z}^{vnesh}\ (2.1)$

Для твердого тела момент инерции тела от времени не зависит, то есть

$J_z\frac{dw_z}{dt}={M_z}^{vnesh}$ (2.2), момент инерции нулю не может быть равен, следовательно, необходимо найти точку на графике, в которой равна нулю производная от угловой скорости. Такой точкой, является точка экстремума, следовательно, $\frac{dw_z}{dt}=0$ в точке 4, отсюда следует, что ${M_z}^{vnesh}=0$ в точке 4.