Уравнения Максвелла
Роль уравнений Максвелла в физике
Система уравнений Максвелла – это, пожалуй, основа электродинамики. Она описывает электромагнитное поле как единое целое, составленное электрическим и магнитным полем. Первое создается вокруг заряженной частицы, движущиеся заряженные частицы (как, например, в токопроводящем проводнике) дают рождение магнитному поле. В то же время магнитное поле воздействует на электрические заряды, находящиеся в движении, и даже тела.
Электрическое поле переносится электроном, а вот носителем магнитного поля является фотон.
Любые ЭМ-волны – микроволны, инфракрасные волны, рентгеновское излучение и даже видимый свет – это всё электромагнитные поля.
Уравнения Максвелла изначально были представлены в дифференциальном виде – для непрерывной среды. Однако в реальности приходится иметь дело с «разрывами» – к примеру, когда среда состоит из разных материалов, и её свойства в какой-то точке резко изменяются.
Первое уравнение Максвелла
Первое из уравнений Максвелла (его также называют законом Гаусса) имеет вид:
![]()
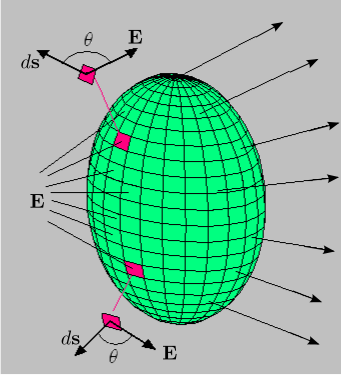
![]() – это электрическая индукция. Её поток протекает через поверхность S, внутри которой в неком объеме заключен электрический заряд Q. Поток электрической индукции через эту поверхность пропорционален заряду внутри объема. Формула говорит нам о том, что электрическое поле «вытекает» из заряда. А электрическая индукция, по сути, характеризирует, насколько напряженное это поле, насколько сильно оно влияет на окружающие объекты.
– это электрическая индукция. Её поток протекает через поверхность S, внутри которой в неком объеме заключен электрический заряд Q. Поток электрической индукции через эту поверхность пропорционален заряду внутри объема. Формула говорит нам о том, что электрическое поле «вытекает» из заряда. А электрическая индукция, по сути, характеризирует, насколько напряженное это поле, насколько сильно оно влияет на окружающие объекты.
Второе уравнение Максвелла
Следующий закон Максвелла напоминает первый (это тоже гауссов закон), но предназначен для магнитного поля:
![]()
![]() — это тоже индукция, но уже электромагнитная. Мы видим, что через замкнутую поверхность её поток нулевой – а это значит, что внутри поверхности нет источников магнитного заряда. Их нет в природе. Одиночные электрические заряды (электроны, позитроны, протоны) в природе существуют, а вот магнитных зарядов с разными полярностями не бывает.
— это тоже индукция, но уже электромагнитная. Мы видим, что через замкнутую поверхность её поток нулевой – а это значит, что внутри поверхности нет источников магнитного заряда. Их нет в природе. Одиночные электрические заряды (электроны, позитроны, протоны) в природе существуют, а вот магнитных зарядов с разными полярностями не бывает.
Третье уравнение Максвелла
Третий закон Максвелла еще называют законом индукции Фарадея:
![]()
![]() – это напряженность электрического поля, циркулирующего по контуру l. l – это граница поверхности s, сквозь которую проходит поток
– это напряженность электрического поля, циркулирующего по контуру l. l – это граница поверхности s, сквозь которую проходит поток ![]() — магнитной индукции. В этом уравнении заложен принцип работы генератора: чем быстрее и сильнее изменяется магнитное поле (например, магнит вращается внутри катушки), тем быстрее раскручивается электрическое поле на границе контура (в случае с генератором – на обмотке индуцируется электрический ток).
— магнитной индукции. В этом уравнении заложен принцип работы генератора: чем быстрее и сильнее изменяется магнитное поле (например, магнит вращается внутри катушки), тем быстрее раскручивается электрическое поле на границе контура (в случае с генератором – на обмотке индуцируется электрический ток).
Четвертое уравнение Максвелла
Четвертый закон Максвелла:
![]()
Здесь мы видим, как рождается магнитное поле. Если сквозь поверхность протекает электрический ток I и проходит поток ![]() электрической индукции, то по границе поверхности будет циркулировать магнитное поле напряженностью
электрической индукции, то по границе поверхности будет циркулировать магнитное поле напряженностью ![]() — и его циркуляция будет пропорциональна их сумма.
— и его циркуляция будет пропорциональна их сумма.
Уравнения Максвелла применяются не только в электротехнике (генераторы и трансформаторы, электрические машины и схемы) – они стали толчком для открытия радиоволн, а чуть позже – толчком для создания теории относительности.
Примеры решения задач
| Задание | Показать, что из уравнений Максвелла следует закон сохранения электрического заряда:
|
| Решение | Запишем четвертое уравнение Максвелла:
Применим к его левой части теорему Стокса: Тогда уравнение примет вид: Выделив подынтегральные выражения, получим: Возьмем дивергенцию от обеих частей: 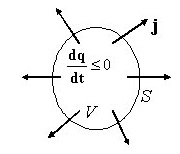
|
| Ответ | получили выражение |
| Задание | Как, зная интегральные уравнения Максвелла, получить их в дифференциальной форме? |
| Решение | 1) Первое уравнение Максвелла имеет вид:
Применим к его левой части теорему Остроградского-Гаусса: А так как полный электрический заряд равен интегралу от его плотности 2) Применим теорему Остроградского ко второму закону Максвелла: 3) Применим теорему Стокса к третьему закону Максвелла, преобразуем его левую часть: Тогда перепишем уравнение в виде: Откуда, в силу произвольности интегрирования: 4) Применяя теорему Стокса, преобразуем левую часть четвертого уравнения Максвелла: Тогда всё уравнение перепишем в виде: |
| Ответ |











