Основное уравнение МКТ

Определение и формула уравнения МКТ

ОПРЕДЕЛЕНИЕ

Уравнение, положенное в основу молекулярно-кинетической теории, связывает макроскопические величины, описывающие состояние идеального газа (например, давление) с параметрами его молекул (их массами и скоростями). Это уравнение имеет вид:

$p=\frac{1}{3} m_0 n\overline{v^2 }$

Здесь $m_0$ – масса газовой молекулы, $n$ – концентрация таких частичек в единице объема, $\overline{v^2 }$ – усреднённый квадрат скорости молекул.

Основное уравнение МКТ наглядно объясняет, каким образом идеальный газ создает давление на окружающие его стенки сосуда. Молекулы все время ударяются о стенку, воздействуя на нее с некоторой силой F. Тут следует вспомнить третий закон Ньютона: когда молекула ударяется о предмет, на нее действует сила -F, вследствие чего молекула «отбивается» от стенки. При этом мы считаем соударения молекул со стенкой абсолютно упругими: механическая энергия молекул и стенки полностью сохраняется, не переходя во внутреннюю энергию тел. Это значит, что при соударениях изменяются только скорости молекул, а нагревания молекул и стенки не происходит.

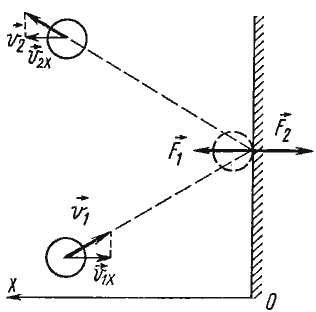
Зная, что соударение со стенкой было упругим, мы можем предсказать, как изменится скорость молекулы после столкновения. Модуль скорости останется таким же, как и до соударения, а направление движения изменится на противоположное относительно оси Ох (считаем, что Ох – это та ось, которая перпендикулярна стенке).

Молекул газа очень много, движутся они хаотично и о стенку ударяются часто. Найдя геометрическую сумму сил, с которой каждая молекула воздействует на стенку, мы узнаём силу давления газа. Чтобы усреднить скорости молекул, необходимо использовать статистические методы. Именно поэтому в основном уравнении МКТ используют усредненный квадрат скорости молекул $\overline{v^2 }$ , а не квадрат усредненной скорости $\bar{v}^2$ : усредненная скорость хаотично движущихся молекул равна нулю, и в этом случае никакого давления мы бы не получили.

Теперь ясен физический смысл уравнения: чем больше молекул содержится в объеме, чем они тяжелее и чем быстрее движутся – тем большее давление они создают на стенки сосуда.

Основное уравнение МКТ для модели идеального газа

Следует заметить, что основное уравнение МКТ выводилось для модели идеального газа с соответствующими допущениями:

Соударения молекул с окружающими объектами абсолютно упругие. Для реальных же газов это не совсем так; часть кинетической энергии молекул всё-таки переходит во внутреннюю энергию молекул и стенки.
Силами взаимодействия между молекулами можно пренебречь. Если же реальный газ находится при высоком давлении и сравнительно низкой температуре, эти силы становятся весьма существенными.
Молекулы считаем материальными точками, пренебрегая их размером. Однако размеры молекул реальных газов влияют на расстояние между самими молекулами и стенкой.
И, наконец, основное уравнение МКТ рассматривает однородный газ – а в действительности мы часто имеем дело со смесями газов. Как, например, воздух.

Однако для разреженных газов это уравнение дает очень точные результаты. Кроме того, многие реальные газы в условиях комнатной температуры и при давлении, близком к атмосферному, весьма напоминают по свойствам идеальный газ.

Как известно из законов динамики, кинетическая энергия любого тела или частицы $E_k =\frac{mv ^2 }{2}$ . Заменив произведение массы каждой из частичек и квадрата их скорости в записанном нами уравнении, мы можем представить его в виде:

$p= \frac{2}{3} nE _k$

Также кинетическая энергия газовых молекул выражается формулой $E_{k} =\frac{3}{2} kT$ , что нередко используется в задачах. Здесь k – это постоянная Больцмана, устанавливающая связь между температурой и энергией. k=1,38•10^-23 Дж/К.

Основное уравнение МКТ лежит в основе термодинамики. Также оно используется на практике в космонавтике, криогенике и нейтронной физике.

Примеры решения задач

ПРИМЕР 1

Задание

Определить скорость движения частиц воздуха в нормальных условиях.

Решение

Используем основное уравнение МКТ, считая воздух однородным газом. Так как воздух на самом деле – это смесь газов, то и решение задачи не будет абсолютно точным.

Давление газа:

$p= \frac{1}{3} m_0 n\overline{v^2 }$

Можем заметить, что произведение $n\cdot m_0$ – это плотность газа, так как n – концентрация молекул воздуха (величина, обратная объему), а m – масса молекулы.

Тогда предыдущее уравнение примет вид:

$p= \frac{1}{3} \rho v ^2$

В нормальных условиях давление равно 10⁵ Па, плотность воздуха 1,29кг/м³ – эти данные можно взять из справочной литературы.

Из предыдущего выражения получим скорость молекул воздуха:

$v= \sqrt{\frac{3p }{\rho } } =\sqrt{\frac{3\cdot 10^5 }{1,29} }= 483 m/c$

Ответ

$v=483$ м/с

ПРИМЕР 2

Задание

Определить концентрацию молекул однородного газа при температуре 300 К и давлении 1 МПа. Газ считать идеальным.

Решение

Решение задачи начнём с основного уравнения МКТ: $p=\frac{1}{3} m_0 n\overline{v^2 }.$ Кинетическая энергия молекул, как и любых материальных частичек: $E_{k} =\frac{mv ^2 }{2}$ . Тогда наша расчетная формула примет несколько другой вид:

$p= \frac{2}{3} nE_{k}$

Однако кинетическая энергия молекул в термодинамике определяется и с помощью другого выражения, и напрямую связана с температурой газа:

$E_{k} =\frac{3}{2} kT$

Подставив эту формулу в предыдущее выражение, получим еще одну форму записи основного уравнения МКТ:

$p=nkT$

Выразим и рассчитаем концентрацию молекул газа:

$n=\frac{p}{kT} =\frac{10^6 }{1,38\cdot 10^{-23} \cdot 300} = 2,42\cdot10^{17} m^{-3}$

Ответ

$n=2,42\cdot10^{17}$ молекул/м $^{3}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Основное уравнение МКТ

Определение и формула уравнения МКТ

Основное уравнение МКТ для модели идеального газа

Примеры решения задач