Уравнение Эйнштейна

ОПРЕДЕЛЕНИЕ

Уравнение Эйнштейна – та самая знаменитая формула релятивистской механики – устанавливает связь между массой покоящегося тела и его полной энергией:

$E=mc^2$

Здесь $Е$ – полная энергия тела (так называемая энергия покоя), $m$ – его масса, а $c$ – скорость света в вакууме, которая приблизительно равна $3 \cdot 10^{8}$ м/с.

Уравнение Эйнштейна

Формула Эйнштейна утверждает, что масса и энергия эквивалентны друг другу. Это значит, что любое тело обладает внутренней энергией – энергией покоя – пропорциональной его массе. В свое время природа затратила энергию, чтобы собрать это тело из элементарных частиц материи, и энергия покоя служит мерой этой работы.

Действительно, при изменении внутренней энергии тела его масса изменяется пропорционально изменению энергии:

$\Delta m= \frac{\Delta E}{c^2} m_{rel} =\frac{m}{\sqrt{1-\frac{v^2}{c^2}}}$

Например, при нагреве тела его внутренняя энергия возрастает, и масса тела увеличивается. Правда, эти изменения настолько малы, что в повседневной жизни мы их не замечаем: при нагреве 1 кг воды на $100^{\circ} C$ она станет тяжелее на 4,7•10^-12 кг.

Кроме того, масса может преобразовываться в энергию, и наоборот. Преобразование массы в энергию происходит при ядерной реакции: масса ядер и частиц, образовавшихся в результате реакции, меньше, чем масса столкнувшихся ядер и частиц, а получившийся дефект массы превращается в энергию. А при фотонном рождении несколько фотонов (энергия) превращаются в электрон, вполне материальный и имеющий массу покоя.

Уравнение Эйнштейна для движущегося тела

Для движущегося тела уравнений Эйнштейна выглядит:

$E=\frac{mc^2}{\sqrt{1-\frac{v^2}{c^2}}}$

В этой формуле v – скорость, с которой движется тело.

Из последней формулы можно сделать несколько важных выводов:

1) Каждое тело, обладает определенную энергию, которая больше нуля. Поэтому $\sqrt{1-\frac{v^2}{c^2}}>0$ , а значит, v

2) Некоторые частицы – например, фотоны – не имеют массы, а вот энергия у них есть. При подстановке $m=0$ в последнюю формулу мы получили бы не соответствующее действительности $Е=0$ , если бы не одно «но»: эти частицы движутся со скоростью света с=3•10⁸ м/с. Знаменатель формулы Эйнштейна при этом обращается в нуль: она не подходит для расчёта энергии безмассовых частиц.

Формула Эйнштейна показала, что в веществе содержится колоссальный запас энергии – и тем самым сыграла неоценимую роль в развитии ядерной энергетики, а также подарила военной промышленности атомную бомбу.

Примеры решения задач

ПРИМЕР 1

Задание

${\pi}^0$ -мезон имеет массу покоя $2,4 \cdot 10^{-28}$ кг и движется со скоростью 0,8с. Какова его кинетическая энергия?

Решение

Найдем скорость $\pi^0$ -мезона в единицах СИ:

$v=0,8c =0,8\cdot 3\cdot 10^8 =2,4\cdot 10^8$ м/с

Рассчитаем энергию покоя $\pi^0$ -мезона по формуле Эйнштейна:

$E_0 =mc^2 =2,4\cdot 10^{-28} \cdot (3\cdot 10^8 )^2 =2,16\cdot 10^{-11}$ Дж

Полная энергия $\pi^0$ -мезона:

$E=\frac{mc^2}{\sqrt{1-\frac{v^2}{c^2}}} =\frac{2,4\cdot 10^{-28} \cdot (3\cdot 10^8 )^2}{\sqrt{1-\frac{2,4\cdot 10^8}{3\cdot 10^8}}} =3,6\cdot 10^{-11}$ Дж

Полная энергия $\pi^0$ -мезона состоит из энергии покоя и кинетической энергии. Поэтому кинетическая энергия:

$E_{k} =E-E_0 =3,6\cdot 10^{-11} -2,16\cdot 10^{-11} =1,44\cdot 10^{-11}$ Дж

Ответ

$E_{k} =1,44\cdot 10^{-11}$ Дж

ПРИМЕР 2

Задание

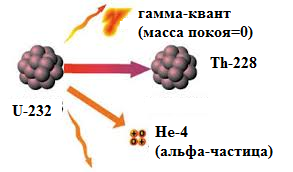
При радиоактивном распаде атома урана массой 232,03714 а.о.м. образовались атом тория массой 228,02872 а.о.м. и атом гелия массой 4,0026 а.о.м. Какая энергия выделилась при распаде?