Уравнение состояния идеального газа
Молекулы свободно движутся и лишь иногда сталкиваются между собой и со стенками сосуда, в котором находятся. Это значит, что в таком газе можно пренебречь потенциальной энергией его молекул в сравнении с кинетической. Газы можно считать идеальными с достаточной степенью точности в тех случаях, когда рассматриваются их состояния, далекие от областей фазовых превращений.
Уравнение состояния идеального газа
Параметры, с помощью которых описывают состояние идеального газа, как макросистемы это давление (p), объем (V), температура по шкале Кельвина (T). Очевидно, что уравнение, которое их связывает, является очень значимым с точки зрения теории и практики. Называется оно уравнением состояния идеального газа (иногда просто уравнением идеального газа):
![]()
где ![]() Дж/К – постоянная Больцмана,
Дж/К – постоянная Больцмана,
![]()
n- число молекул в единице объема газа ( концентрация частиц вещества), N — число его молекул в заданном объеме.
Уравнению (1) можно придать известную форму уравнения Клапейрона (Надо отметить, что от изменения формы записи уравнения (2), (3) не перестают быть уравнениями состояния идеального газа):
![]()
или
![]()
где ![]() — количество молей газа, R
— количество молей газа, R![]() =8,3 Дж/(моль•К) – молярная (универсальная) газовая постоянная, (
=8,3 Дж/(моль•К) – молярная (универсальная) газовая постоянная, (![]() моль-1 (постоянная Авогадро)),
моль-1 (постоянная Авогадро)), ![]() – молярная масса газа,
– молярная масса газа, ![]() – плотность газа.
– плотность газа.
Уравнение состояния для смеси газов
Если газ представляет собой смесь газов, то уравнение (состояния) идеального газа принимает вид:
![]()
где![]() число молей i-го компонента смеси.
число молей i-го компонента смеси.
Для произвольной массы газа (m) с молярной массой ![]() уравнение (состояния) идеального газа имеет вид:
уравнение (состояния) идеального газа имеет вид:
![]()
Это уравнение называют уравнением Менделеева – Клапейрон и оно, опять таки, является уравнением идеального газа, точнее одной из форм записи этого уравнения.
Примеры решения задач
| Задание | В баллоне содержится газ под давлением |
| Решение | Прежде всего, необходимо все имеющиеся данные перевести в систему СИ, так получим:
давление воздуха:
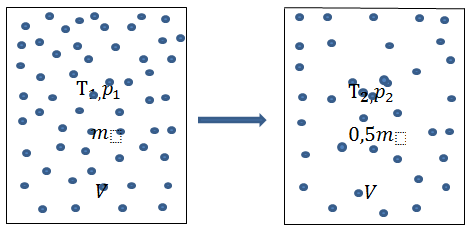
рис. 1. Запишем уравнение состояния идеального газа в виде уравнения Менделеева-Клайперона. В данном случае его использовать удобнее, так как в нем в явном виде присутствует масса газа. Для первого состояния имеем: для второго состояния имеет: Разделим уравнение (1.1.) на уравнение (1.2.). Получим: Выразим искомую Проведем расчет искомой температуры, подставим численные значения в формулу (1.3.): |
| Ответ | Искомая температура 300 К |
| Задание | Закрытый цилиндр длиной l разделен на две части теплонепроницаемым поршнем. В обеих половинах находятся одинаковые массы одного и того же газа при температуре 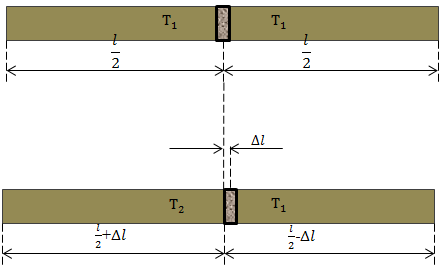
рис. 2 |
| Решение | Запишем уравнение идеального газа для левой части сосуда (используем форму (5)).
До нагревания После нагревания: Разделим (2.2) на (2.1), получим: или Для второй части сосуда: После того как нагрели соседнюю часть сосуда: Из (2.4), (2.5) получаем: Левые части выражений (2.3) и (2.6.) равны, соответственно равны и правые: где V=S учтем, что поршень сместится на такое расстояние при котором давления в правой и левой частях будут равны ( Тогда |
| Ответ | Поршень сместится на расстояние |











