Уравнение диффузии

ОПРЕДЕЛЕНИЕ

Явлением диффузии называется процесс установления внутри фаз равновесного распределения концентраций.

Результатом диффузии при постоянной температуре является выравнивание химических потенциалов. В однофазной системе при постоянной температуре и при отсутствии внешних сил диффузия выравнивает концентрацию компонента фазы во всей системе. Если на систему действуют внешние силы или поддерживается градиент температуры, то в результате диффузии устанавливаются градиенты концентраций отдельных компонентов (термодиффузия, электродиффузия и другие процессы).

Уравнение диффузии в одномерном случае

Уравнение диффузии в одномерном случае ( $\rho =\rho \left(x\right)$ ) в двухкомпонентной системе — это первый закон Фика:

$dm=-D\frac{d\rho }{dx}dSdt\ \left(1\right)$

где dm – масса первого компонента, которая переносится за время dt через элементарную площадку dS в направлении нормали x к рассматриваемой площадке в сторону убывания плотности первого компонента, $\frac{d\rho }{dx}$ – градиент плотности, D – коэффициент диффузии.

Если в однокомпонентной системе выделить группу молекул, выравнивание концентрации выделенных частиц по объёму сосуда называется самодиффузией. Самодиффузия тоже описывается уравнением диффузии (первым законом Фика), в котором коэффициент D- называется коэффициентом самодиффузии.

Уравнение диффузии в трехмерном случае

В случае трехмерной диффузии изменение концентрации с течением времени при постоянной температуре и отсутствии внешних сил описывается дифференциальным уравнением диффузии:

$\frac{\partial c}{\partial t}=\frac{\partial }{\partial x}\left(D\frac{\partial c}{\partial x}\right)+\frac{\partial }{\partial y}\left(D\frac{\partial c}{\partial y}\right)+\frac{\partial }{\partial z}\left(D\frac{\partial c}{\partial z}\right) \qquad (2)$

где D- коэффициент диффузии, t- время. Если D не зависит от концентрации, то уравнение диффузии будет иметь вид:

$\frac{\partial c}{\partial t}=D\Delta c\ \left(3\right)$

Уравнение (3) еще называют вторым законом Фика, где $\Delta$ — дифференциальный оператор Лапласа.

В том случае, если перенос вещества вызван лишь градиентом его концентрации уравнение диффузии можно записать и в следующем виде:

$\frac{dc}{dt}=div\left(Dgrad\left(c\right)\right)-q\ \cdot c+F \qquad (4)$

где c(x, t) — концентрация вещества в точке $x=(x_1,x_2,x_3)$ среды в момент времени t, D – коэффициент диффузии, q — коэффициент поглощения, a F — интенсивность источников вещества. Величины D, q и F обычно являются функциями координат и времени, а также могут зависеть от концентрации с(x, t). B последнем случае, уравнение диффузии (4) становится нелинейным. В анизотропной среде коэффициент диффузии D является тензорным полем. В случае, когда величины D и q постоянны уравнение (4) является уравнением параболического типа. Для такого типа уравнений в математической физике разработаны методы решения. Допущение о постоянстве коэффициента диффузии справедливо в большинстве случаев реализуемых на практике. Уравнения диффузии не содержат ни каких сведений о механизмах этого процесса. Основная цель решения уравнения — найти распределение примеси c(x,t) после диффузии в течение определенного времени при различных условиях осуществления процесса.

Решение уравнения диффузии

Для выделения единственного решения для уравнения (4) необходимо задать начальные и граничные условия. Обычно, рассматривают следующие граничные условия:

1) на границе поверхности S поддерживается заданное распределение вещества $c_0(x,t):\ {\left.c(x,t)\right|}_s=c_0(x,t)$

2)на границе поверхности S поддерживается заданная плотность потока вещества, входящего в V через границу S: $-D{\left.\frac{\partial c\left(x,t\right)}{\partial n}\right|}_s=c_1\left(x,t\right),$

где n – внутренняя нормаль к поверхности S $;$

3) S- полупроницаема, и диффузия во внешнюю среду с заданной концентрацией $c_0(x,t)$ через поверхность S происходит по линейному закону: $k\frac{\partial c(x,t)}{\partial n}+h[{\left.c\left(x,t\right)-c_0(x,t)]\right|}_s=0$

В простейшем случае, когда диффузия происходит только вдоль одной прямой и c=c(x,t)уравнение (3) запишется в виде:

$\frac{\partial c}{\partial t}=D\frac{{\partial }^2c}{\partial x^2}\ \left(3\right);t>0\ \left(5\right)$

с начальным условием: $c\left(x,0\right)=\varphi \left(x\right),\ -\infty <x<\infty .$

Тогда уравнение (5) имеет решение вида:

$c\left(x,t\right)=\int^{\infty }_{-\infty }{G\left(x,x',t\right)\varphi \left(x'\right)dx'\ }\left(6\right)$

$G\left(x,x',t\right)=({4\pi Dt)}^{-\frac{1}{2}}{\exp \left[-\frac{{\left(x'-x\right)}^2}{4Dt}\right]\ }$

$x'$ — текущая координата интегрирования.

Выражение (6) называется фундаментальным решением уравнения диффузии в случае (5).

Примеры решения задач

ПРИМЕР 1

Задание

Найти массу газа ( $\Delta m)$ с молярной плотностью $\mu ,$ прошедшего вследствие диффузии через площадку $\Delta S$ за время $\Delta t$ , если градиент плотности в направлении, перпендикулярном площадке, равен $\frac{\Delta \rho }{\Delta t}$ . Температура газа T, средняя длинна свободного пробега молекулы $\lambda$ .

Решение

Запишем первый закон Фика в терминах условий задачи:

$\Delta m=-D\frac{\Delta \rho }{\Delta x}\Delta S\Delta t\qquad (1.1)$

Знак минус означает, направление вектора плотности. Возьмем модуль от правой части выражения (1.1):

$\Delta m=D\frac{\Delta \rho }{\Delta x}\Delta S\Delta t\qquad (1.2)$

Зная, что $D=\frac{1}{3}\overline{\lambda }\overline{v}$ , где $\overline{\lambda }$ — средняя длина свободного пробега молекулы, $\overline{v}$ — средняя скорость молекулы газа и она равна: $v=\sqrt{\frac{8RT}{\pi \mu }}$ .

Соответственно преобразуем (1.2), найдем искомую массу газа:

$\Delta m=\frac{1}{3}\overline{\lambda }\sqrt{\frac{8RT}{\pi \mu }}\frac{\Delta \rho }{\Delta x}\Delta S\Delta t$

Ответ

Искомая масса газа может быть найдена по формуле: $\Delta m=\frac{1}{3}\overline{\lambda }\sqrt{\frac{8RT}{\pi \mu }}\frac{\Delta \rho }{\Delta x}\Delta S\Delta t$

ПРИМЕР 2

Задание

Найти распределение концентрации внутри полубесконечного тонкого цилиндрического сосуда (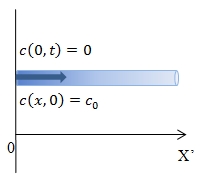 $c(o,t)=0),$ если начальное распределение концентрации вещества: $c\ \left(x,0\right)=f\left(x\right)=c_0$

рис. 1

Решение

Из условий задачи следует, что необходимо найти решение уравнения диффузии $\frac{\partial c}{\partial t}=D\frac{{\partial }^2c}{\partial x^2}$ , удовлетворяющее начальному условию: $c\ \left(x,0\right)=f\left(x\right)=c_0,$ и граничному условию: $c(o,t)=0.$

Решение может быть найдено из фундаментального решения уравнения теплопроводности:

$c\left(x,t\right)=\int^{\infty }_{\infty }{G\left(x,x',t\right)f\left(x'\right)dx'\ },\qquad (2.1)$

где $G\left(x,x',t\right)=({4\pi Dt)}^{-\frac{1}{2}}{\exp \left[-\frac{{\left(x'-x\right)}^2}{4Dt}\right]\ }$

Перепишем (2.1) в виде:

$c\left(x,t\right)=({4\pi Dt)}^{-\frac{1}{2}}\int^{\infty }_0{\{f\left(x'\right){exp \left[-\frac{{\left(x'-x\right)}^2}{4Dt}\right]\ }+}f\left({-x}'\right){exp \left[-\frac{{\left(x'+x\right)}^2}{4Dt}\right]\ }\}d{x}^{'}\qquad (2.2)$

Удовлетворяя граничному условию, будем иметь:

$c\left(0,t\right)=({4\pi Dt)}^{-\frac{1}{2}}\int^{\infty }_0{{exp \left[-\frac{{x'}^2}{4Dt}\right]\ }}\cdot \{f\left(x'\right)-f\left({-x}'\right)\}dx'\qquad (2.3)$

Условие будет выполнено, если $f\left({-x}'\right)=-f\left(x'\right)\ \left(0\le x'\le \infty \right)$ (2.4)

Подставим (2.4) в (2.2) получим:

$c\left(x,t\right)=({4\pi Dt)}^{-\frac{1}{2}}\int^{\infty }_0{f\left(x'\right)\{{exp \left[-\frac{{\left(x'-x\right)}^2}{4Dt}\right]\ }-}{exp \left[-\frac{{\left(x'+x\right)}^2}{4Dt}\right]\ }\}dx'\qquad (2.5)$

Зная, что начальная концентрация постоянна и равна $c_0$ , то из (2.5) получим:

$c\left(x,t\right)=\frac{c_0}{\sqrt{4\pi Dt}}\int^{\infty }_0{\{{exp \left[-\frac{{\left(x'-x\right)}^2}{4Dt}\right]\ }-}{exp \left[-\frac{{\left(x'+x\right)}^2}{4Dt}\right]\ }\}dx'\qquad (2.5)$

Разобьем интеграл на два слагаемых и введем новые переменные интегрирования:

$\alpha =\frac{x'-x}{\sqrt{4Dt}},\ \beta =\frac{x'+x}{\sqrt{4Dt}}\qquad (2.6)$

получим:

$c\left(x,t\right)=\frac{c_0}{\sqrt{\pi }}\left[\int^{\infty }_{-\frac{x}{\sqrt{4Dt}}}{e^{-{\alpha }^2}d\alpha }-\int^{\infty }_{\frac{x}{\sqrt{4Dt}}}{e^{-{\beta }^2}d\beta }\right]=\frac{c_0}{\sqrt{\pi }}\int^{\frac{x}{\sqrt{4Dt}}}_{-\frac{x}{\sqrt{4Dt}}}{e^{-{\alpha }^2}d\alpha }=\frac{{2c}_0}{\sqrt{\pi }}\int^{\frac{x}{\sqrt{4Dt}}}_0{e^{-{\alpha }^2}d\alpha }$

или

$c\left(x,t\right)=c_0\theta \left(\frac{x}{\sqrt{4Dt}}\right),\qquad (2.7)$

где $\theta \left(z\right)=\frac{2}{\sqrt{\pi }}\int^z_0{e^{-{\alpha }^2}}d\alpha$ (2.8)

— интеграл ошибок.