Центр тяжести и центр масс тела
Центр тяжести тела
Положение центра тяжести тела можно определить экспериментально. Для этого достаточно поочередно подвесить тело за две различные точки на его поверхности и провести через точки подвеса вертикали. Пересечение этих линий — линий действия сил тяжести — и определяет положение центра тяжести тела.
Центр масс тела
Координаты центра масс определяются формулами:
![]()
![]()
У однородных симметричных тел центр масс располагается в геометрическом центре тела: у круга (сферы) в его центре, у треугольника — в точке пересечения медиан, у прямоугольника — в точке пересечения диагоналей.
Механическая система всегда находится в равновесии относительно оси вращения, проходящей через ее центр масс.
В отличие от центра тяжести центр масс имеет смысл для любого тела или механической системы в то время, как центр тяжести — только для твердого тела, находящегося в однородном гравитационном поле.
Примеры решения задач
| Задание | Два шара массами 3 и 5 кг скреплены стержнем, масса которого 2 кг. Определить положение общего центра масс системы, если радиус первого шара 5 см, радиус второго шара 7 см, а длина стержня 30 см. |
| Решение | Выполним рисунок.
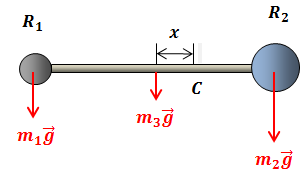
Запишем условие равновесия системы относительно оси, проходящей через ее центр масс Моменты, созданные силами тяжести: Подставим значения моментов в условие равновесия: Переведем единицы в систему СИ: Вычислим: |
| Ответ | Центр тяжести системы находится на расстоянии 5 см от середины стержня в сторону большего шара. |











