Уравнение Эйлера

ОПРЕДЕЛЕНИЕ

Уравнение Эйлера – это уравнение гидродинамики, которое описывает движение потока идеальной жидкости и учитывает силы, воздействующие на жидкость.

В модели Эйлера рассматривается идеальная жидкость, в которой отсутствуют теплопроводность (жидкость имеет постоянную температуру, не нагревается и не охлаждается) и вязкость (в жидкости не возникают силы трения). Поэтому силы, воздействующие на такую жидкость, сводятся к силам давления её собственных масс, гравитационным и инерционным силам.

Уравнение Эйлера в векторной форме

В векторной форме уравнение Эйлера имеет вид:

$\frac{d\bar{v}}{dt } =\bar{g}-\frac{1}{\rho } grad\; p$

Слагаемые в правой части учитывают влияние внешних сил и давления собственной массы жидкости: $\bar{g}(x, y, z, t)$ – напряженность внешнего силового поля, $p(x, y, z, t)$ – давление в жидкости, $\rho$ – плотность жидкости. Вектор $\overline{v}(x, y, z, t)$ – скорость движения жидкости. $\frac{d\bar{v}}{dt }$ – субстанциональная производная, которая представляет собой ускорение движущейся точки в материальной среде. Субстанциональную производную можно разложить на частные производные, и тогда уравнение Эйлера примет вид:

$\frac{\partial \bar{v}}{\partial t} +grad\; v ^2 +rot\; \overline{v}\times \overline{v}=\bar{g}-\frac{1}{\rho } grad\; p$

Последнее уравнение еще называют уравнением движения невязкой жидкости в форме Громеко. Оно удобно еще и тем, что выделяет вихревую составляющую движения в виде слагаемого $rot\; \overline{v}\times \overline{v}$ , а частная производная по времени $\frac{\partial \bar{v}}{\partial t}$ отображает местное ускорение, характерное для неустановившихся течений.

Решение уравнения Эйлера

При расчётах удобнее использовать уравнение Эйлера в скалярной форме:

$\frac{dv _{x} }{dt } =g_{x} -\frac{1}{\rho } grad\; p _{x} ,$

$\frac{dv _{y} }{dt } =g_{y} -\frac{1}{\rho } grad\; p _{y} ,$

$\frac{dv _{z} }{dt } =g_{z} -\frac{1}{\rho } grad\; p _{z} ,$

где векторы скорости и внешних сил, а также поле давления разложены в виде проекций на координатные оси.

При решении несложных прикладных задач гидро- и газодинамики иногда бывает достаточно рассмотреть установившийся во времени одномерный поток. В этом случае уравнение Эйлера примет простой вид:

$v\frac{dv }{dx } =-\frac{1}{\rho } \cdot \frac{dp }{dx }$

Проинтегрировав это выражение, можно получить уравнение Бернулли:

$\frac{\rho v ^2 }{2} +p=const$

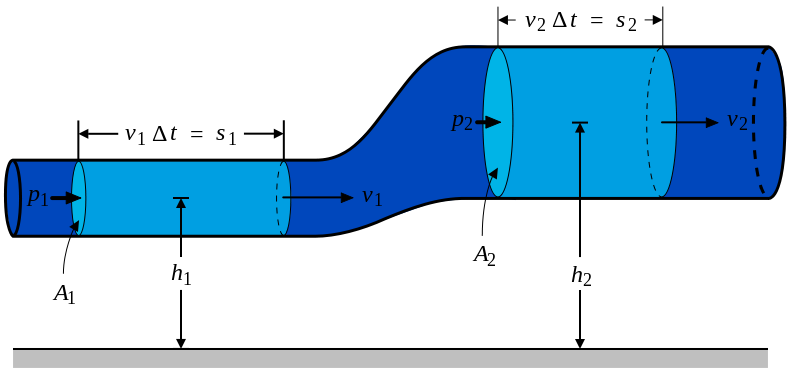
Уравнение Эйлера, лежащее в основе гидродинамики, используется в самых разных областях: при проектировании самолётов и судов, при расчёте турбин, насосов и трубопроводов, при исследовании морских течений и движения грунтовых вод.

Примеры решения задач

ПРИМЕР 1

Задание

По горизонтальной трубе протекает жидкость плотностью 950 кг/м³. Давление на входе в трубу 0,3 МПа, на выходе из трубы 1 МПа. Скорость на входе в трубу 50 м/с. Определить скорость на выходе из трубы.

Решение

Запишем уравнение Эйлера для стационарного одномерного потока:

$v\frac{dv }{dx } =-\frac{1}{\rho } \cdot \frac{dp }{dx }$

Умножим обе части на dx и проинтегрируем:

$vdv =-\frac{dp }{\rho }$

$\frac{\rho v ^2 }{2} +p=const$

Запишем это выражение для входного и выходного сечений:

$\frac{\rho v _1 ^2 }{2} +p_1 =\frac{\rho v _2 ^2 }{2} +p_2 ,$

$\frac{\rho (v _1 ^2 -v_2 ^2 )}{2} =p_2 -p_1 ,$

$v_2 =\sqrt{v_1 ^2 -\frac{2(p _2 -p_1 )}{\rho } } =\sqrt{50^2 -\frac{2\cdot (10 ^6 -3\cdot 10^5 )}{950} } =32,04 \ m/c$

Ответ

$v_2 = 32,04$ м/с

ПРИМЕР 2

Задание

Получите вывод уравнения Эйлера.

Решение

Пусть объем жидкости постоянно состоит из одних и тех же частиц. Запишем для него II закон Ньютона:

$\frac{d}{dt } \iiint_{V}\rho \overline{v}dV= \overline{F}+\overline{F}_{S}$

где $\overline{F}=\iiint_{V}\rho \overline{g}dV$ — внешняя объемная сила, $\overline{F}_{S} =- \oint\int _{S}\overline{n}pdS=- \iiint_{V}\nabla pdV$ — сила, действующая на объем $V$ со стороны окружающей среды через ограничивающую поверхность $S$ .

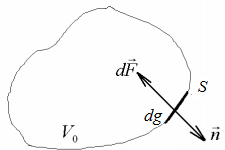
Подставив эти выражения в первый интеграл, получим:

$\iiint \nolimits _{V}\left[\frac{d(\rho \overline{v})}{dt } +\rho \overline{v}(\nabla \overline{v})\right] dV= \iiint \nolimits _{V}\left[-\nabla p+\rho \overline{g}\right] dV$

Поскольку объем $V$ был выбран произвольно, этот интеграл можно решить как несобственный:

$\rho \frac{d\overline{v}}{dt } +\overline{v}\frac{d\rho }{dt } +\rho \overline{v}(\nabla \overline{v})=- \nabla p+\rho \overline{g}$

Используем уравнение неразрывности $\frac{\partial \rho }{\partial t} +\nabla (\rho \overline{v})=0$ :

$\overline{v}\frac{d\rho }{dt } +\rho \overline{v}(\nabla \overline{v})=0$

вследствие чего приходим к форме записи:

$\frac{\partial \overline{v}}{\partial t} +(\overline{v}\nabla )\overline{v}=- \frac{\nabla p}{\rho } +\overline{g}$

Ответ

Получено уравнение Эйлера: $\frac{\partial \overline{v}}{\partial t} +(\overline{v}\nabla)\overline{v}=- \frac{\nabla p}{\rho } +\overline{g}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Уравнение Эйлера

Уравнение Эйлера в векторной форме

Решение уравнения Эйлера

Примеры решения задач