Импульс тела. Закон сохранения импульса

Определение импульса тела

ОПРЕДЕЛЕНИЕ

Импульс (количество движения) тела – это произведение массы тела $m$ на скорость его движения $\overline{v}$ , т.е. величина $m\overline{v}$ .

Импульс $\overline{p}$ — величина векторная, совпадающая по направлению с вектором скорости $\overline{v}$ .

Единица измерения импульса в системе СИ: кг • м/с .

Импульс системы тел равен векторной сумме импульсов всех тел, входящих в систему:

$\overline{p}=\sum^n_{i=1}{{\overline{p}}_i\ }$

ОПРЕДЕЛЕНИЕ

Импульс силы – это величина, равная произведению силы на время ее действия, т.е. величина $\overline{F}\Delta t$ .

Закон сохранения импульса

Если на систему взаимодействующих тел действуют дополнительно внешние силы, например, силы трения, то в этом случае справедливо соотношение, которое иногда называют законом изменения импульса:

изменение импульса системы тел равно векторной сумме импульсов всех внешних сил, действующих на систему:
$\Delta \overline{p}=\sum^n_{i=1}{{\overline{F}}_i\Delta t}$

Для замкнутой системы (при отсутствии внешних сил) справедлив закон сохранения импульса:

импульс замкнутой системы есть величина постоянная:
$\overline{p}=const$

Действием закона сохранения импульса можно объяснить явление отдачи при стрельбе из винтовки или при артиллерийской стрельбе. Также действие закона сохранения импульса лежит в основе принципа работы всех реактивных двигателей.

При решении физических задач законом сохранения импульса пользуются, когда знание всех деталей движения не требуется, а важен результат взаимодействия тел. Такими задачами, к примеру, являются задачи о соударении или столкновении тел. Законом сохранения импульса пользуются при рассмотрении движения тел переменной массы таких, как ракеты-носители. Большую часть массы такой ракеты составляет топливо. На активном участке полета это топливо выгорает, и масса ракеты на этом участке траектории быстро уменьшается. Также закон сохранения импульса необходим в случаях, когда неприменимо понятие «ускорения». Трудно себе представить ситуацию, когда неподвижное тело приобретает некоторую скорость мгновенно. В обычной практике тела всегда разгоняются и набирают скорость постепенно. Однако при движении электронов и других субатомных частиц изменение их состояния происходит скачком без пребывания в промежуточных состояниях. В таких случаях классическое понятие «ускорения» применять нельзя.

Примеры решения задач

ПРИМЕР 1

Задание

Снаряд массой 100 кг, летящий горизонтально вдоль железнодорожного пути со скоростью 500 м/с, попадает в вагон с песком массой 10 т и застревает в нем. Какую скорость получит вагон, если он двигался со скоростью 36 км/ч в направлении, противоположном движению снаряда?

Решение

Система вагон+снаряд является замкнутой, поэтому в данном случае можно применить закон сохранения импульса.

Выполним рисунок, указав состояние тел до и после взаимодействия.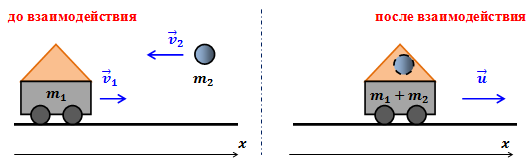

При взаимодействии снаряда и вагона имеет место неупругий удар. Закон сохранения импульса в этом случае запишется в виде:

$m_1{\overline{v}}_1+m_2{\overline{v}}_2=\left(m_1+m_2\right)\overline{u}\$

Выбирая направление оси $x$ совпадающим с направлением движения вагона, запишем проекцию этого уравнения на координатную ось:

$m_1v_1-m_2v_2=\left(m_1+m_2\right)u$

откуда скорость вагона после попадания в него снаряда:

$u=\frac{m_1v_1-m_2v_2}{m_1+m_2}$

Переводим единицы в систему СИ: $m_{1}=10$ т $=10000$ кг.

$v_{1}=36$ км/ч $= 10$ м/с

Вычислим:

$u=\frac{10000\cdot 10-100\cdot 500}{10000+100}=5\ {m}/{c}$

Ответ

После попадания снаряда вагон будет двигаться со скоростью 5 м/с.

ПРИМЕР 2

Задание

Снаряд массой m=10 кг обладал скоростью v=200 м/с в верхней точке траектории. В этой точке он разорвался на две части. Меньшая часть массой m₁=3 кг получила скорость v₁=400 м/с в прежнем направлении под углом $\varphi ={60}^\circ$ к горизонту. С какой скоростью и в каком направлении полетит большая часть снаряда?

Решение

Траектория движения снаряда – парабола. Скорость тела всегда направлена по касательной к траектории. В верхней точке траектории скорость снаряда параллельна оси 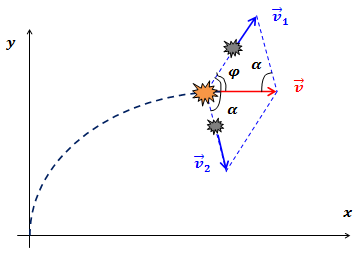$x$ .

Запишем закон сохранения импульса:

$m\overline{v}=m_1{\overline{v}}_1+m_2{\overline{v}}_2$

или

$m_2{\overline{v}}_2=m\overline{v}-m_1{\overline{v}}_1\$

Перейдем от векторов к скалярным величинам. Для этого возведем обе части векторного равенства в квадрат и воспользуемся формулами для скалярного произведения векторов:

${m_2}^2{v_2}^2=m^2v^2-2mm_1vv_1\cos\varphi +{m_1}^2{v_1}^2\$

Учитывая, что $\cos\varphi =\cos{60}^\circ=\frac{1}{2}$ , а также что $m_2=m-m_1$ , находим скорость второго осколка:

$v_2=\frac{\sqrt{m^2v^2-mm_1vv_1+{m_1}^2{v_1}^2}}{{m-m}_1}$

Подставив в полученную формулу численные значения физических величин, вычислим:

$v_2=\frac{\sqrt{{10}^2\cdot {200}^2-10\cdot 3\cdot 200\cdot 400+3^2\cdot {400}^2}}{10-3}=249\ m/c$

Направление полета большей части снаряда определим, воспользовавшись теоремой синусов:

$\frac{\sin\alpha }{v_1}=\frac{\sin\varphi }{v_2}\$

откуда

$\sin\varphi =\frac{v_2}{v_1}\cdot \sin\alpha \$

Подставив в формулу численные значения, получим:

$\sin\varphi =\frac{249}{400}\cdot {\sin {60}^\circ=0,5391\ }$

$\varphi =\text{arcsin}(0,5391)={33}^\circ\$

Ответ

Большая часть снаряда полетит со скоростью 249 м/с вниз под углом ${33}^\circ$ к горизонтальному направлению.

ПРИМЕР 3

Задание

Масса поезда 3000 т. Коэффициент трения 0,02. Какова должна быть сила тяги паровоза, чтобы поезд набрал скорость 60 км/ч через 2 мин после начала движения.

Решение

Так как на поезд действует сила трения (внешняя сила), систему нельзя считать замкнутой, и закон сохранения импульса в данном случае не выполняется.

Воспользуемся законом изменения импульса:

$\Delta \overline{p}=\left(\overline{F}+{\overline{F}}_{fr}\right)\Delta t$

Так как сила трения всегда направлена в сторону, противоположную движению тела, в проекцию уравнения на ось координат (направление оси совпадает с направлением движения поезда) импульс силы трения войдет со знаком «минус»:

$\Delta p=\left(F-F_{fr}\right)\Delta t$