Формула момента инерции

Момент инерции тела

ОПРЕДЕЛЕНИЕ

Момент инерции $(J)$ относительно оси, вокруг которой происходит вращение – это мера инертности тела, совершающего вращательные движения.

Момент инерции является скалярной (в общем случае тензорной) физической величиной, которую находят как сумму произведений масс материальных точек ( $\Delta m_i$ ) (на которые следует провести разбиение рассматриваемого тела) на квадраты расстояний ( $r^2_i$ ) от них до оси вращения:

$J=\sum^k_{i=1}{{\Delta m}_ir^2_i} \qquad (1)$

Если тело считают непрерывным, то суммирование в выражении (1) заменяется интегрированием, массы элементов тела обозначают как $dm$ :

$J=\int_m{r^2dm=\int_V{r^2}\rho dV} \qquad (2)$

где r – функция положения материальной точки в пространстве; $\rho$ – плотность тела; $dV$ –объем элемента тела. Если тело является однородным:

$\ J=\rho \int_V{r^2}dV\ \qquad(3)$

Момент инерции материальной точки

Роль массы при движении по окружности материальной точки выполняет момент инерции (J), который равен:

$J=mr^2 \qquad(4)$

где r- расстояние от материальной точки до оси вращения. Для материальной точки, которая движется по окружности, момент инерции является постоянной величиной.

Момент инерции является аддитивной величиной. Это означает то, что если в системе не одна, а несколько материальных точек, то момент инерции системы (J) равен сумме моментов инерции ( $J_i$ ) отдельных точек:

$J=\sum^N_{i=1}{J_i}\ \qquad(5)$

Примеры моментов инерции некоторых тел

Момент инерции тонкого стержня вращающегося около оси, проходящей через его один конец и перпендикулярно стержню, равен:

$J=\frac{1}{3}ml^2 \qquad(6)$

Момент инерции прямого круглого конуса, массы $m,$ высоты h и радиуса r вращающегося около своей оси:

$J=0,3mr^2 \qquad(7)$

Момент инерции однородного твердого параллелепипеда, c геометрическими параметрами $d,w,l$ и массой m вращающегося относительно своей самой длинной диагонали, вычисляют по формуле:

$J=\frac{m{(w}^2d^2+{l^2d}^2+{l^2w}^2)}{6(l^2+w^2+d^2)} \qquad(8)$

Момент инерции тонкой прямоугольной пластины массы m, ширины w и длины d, вращающейся относительно оси, которая проходит через точку пересечения диагоналей этого прямоугольника перпендикулярно плоскости пластины:

$J=\frac{m(w^2+d^2)}{12} \qquad(9)$

где m – масса шара; R – радиус шара. Шар вращается около оси, которая проходит через его центр.

Примеры формул для вычисления моментов инерции других тел можно посмотреть в разделе «Момент инерции». В этом же разделе можно ознакомиться с теоремой Штейнера.

Примеры решения задач по теме «Момент инерции»

ПРИМЕР 1

Задание

Два малых шарика массой m каждый соединены тонким невесомым стержнем, длина которого равна 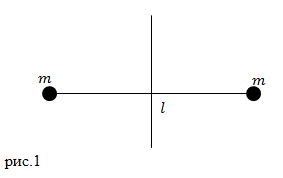$l.$ Каким будет момент инерции системы относительно оси, которая проходит перпендикулярно стержню через центр масс сиcтемы?

Решение

Для решения задачи используем формулу для момента инерции одной материальной точки:

$J_1=mr^2 \qquad(1.1)$

где расстояние от точки до оси вращения равно $r=\frac{l}{2}$ . Следовательно, формула (1.1) преобразуется к виду:

$J_1=m{\left(\frac{l}{2}\right)}^2 \qquad(1.2)$

Так как массы первой и второй материальных точек равны, равны расстояния от каждой из них до оси вращения, то:

$J_1=J_2 \qquad(1.3)$

Момент инерции является аддитивной величиной, значит, момент инерции двух точек найдем как сумму $J_1$ и $J_2$ :

${J=J}_1+J_2=2\cdot m{\left(\frac{l}{2}\right)}^2=m\frac{l^2}{2}$

Ответ

$J=m\frac{l^2}{2}$

ПРИМЕР 2

Задание

Каков момент инерции системы, которая изображена на рис.2 и состоит из двух тонких стержней с массами m. Угол между стержнями прямой. Длины стержней равны l. Ось вращения параллельна одному из стержней (рис.2).

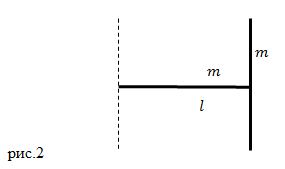
Решение

Момент инерции системы можно найти как сумму моментов инерции каждого стержня относительно оси вращения:

${J=J}_1+J_2\ \qquad(2.1)$

Момент инерции ( $J_1$ ) для горизонтального стержня равен:

$J_1=\frac{1}{3}ml^2 \qquad(2.2)$

Найдем момент инерции для стержня параллельного оси вращения. Для этого выделим на этом стержне материальную точку массы $dm$ . Для нее момент инерции относительно указанной на рис.2 оси равен:

$dJ=dml^2 \qquad(2.3)$

где l – расстояние по горизонтали от массы $dm$ до оси вращения, оно при движении по стержню не изменяется.

Найдем момент инерции всего стержня ( $J_2$ ) для этого просуммируем подобные (2.3) элементарные моменты инерции, а так как стержень непрерывный, то вместо суммы возьмем интеграл:

$J_2=\int{dml^2}=l^2\int{dm=ml^2} \qquad (2.4)$

Найдем искомый момент инерции системы стержней:

$J=\frac{1}{3}ml^2+ml^2=\frac{4}{3}ml^2$