Момент инерции материальной точки
Для динамического описания движения материальной точки по окружности используют следующие величины: момент силы (![]() ), момент импульса (
), момент импульса (![]() ) и момент инерции (J). При этом основной закон динамики вращательного движения записывают в виде:
) и момент инерции (J). При этом основной закон динамики вращательного движения записывают в виде:
![]()
Кроме этого, описывая движение по окружности вместо радиус-вектора (![]() ) пользуются углом поворота (
) пользуются углом поворота (![]() ), вместо вектора скорости (
), вместо вектора скорости (![]() ) используют вектор угловой скорости (
) используют вектор угловой скорости (![]() ).
).
Момент инерции
Роль массы при движении по окружности материальной точки выполняет момент инерции (J), который равен:
![]()
где r- расстояние от материальной точки до оси вращения. Для материальной точки, которая движется по окружности, момент инерции является постоянной величиной. При этом изменение момента импульса происходит только за счет изменения угловой скорости:
![]()
Используя момент инерции основное уравнение динамики (1) для движения материальной точки по окружности можно записать как:
![]()
где ![]() – угловое ускорение материальной точки. Уравнение (4) отражает тот факт, что при движении материальной точки по окружности, момент силы исполняет роль силы (в поступательном движении), момент инерции – роль массы, угловое ускорение – роль линейного ускорения. Это легко увидеть, если записать второй закон Ньютона и сравнить его с уравнением (4):
– угловое ускорение материальной точки. Уравнение (4) отражает тот факт, что при движении материальной точки по окружности, момент силы исполняет роль силы (в поступательном движении), момент инерции – роль массы, угловое ускорение – роль линейного ускорения. Это легко увидеть, если записать второй закон Ньютона и сравнить его с уравнением (4):
![]()
Мерой инертности материальной точки при движении по окружности служит момент инерции.
Момент инерции является аддитивной величиной. Это означает то, что если в системе не одна, а несколько материальных точек, то момент инерции системы (J) равен сумме моментов инерции (![]() ) отдельных точек:
) отдельных точек:
![Rendered by QuickLaTeX.com \[J=\sum^N_{i=1}{J_i}=\sum^N_{i=1}{\Delta m_ir^2_i} \qquad (6)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b7cb11aa532794f163041196f1ac0bf7_l3.png)
где ![]() – масса
– масса ![]() ой материальной точки;
ой материальной точки; ![]() расстояние от данной материальной точки до оси вращения. Момент инерции системы материальных точек зависит от распределения этих точек в пространстве. Чем ближе материальные точки находятся от оси вращения, тем меньше момент инерции данной системы. У твёрдых тел, которые можно представить как непрерывную совокупность материальных точек, момент инерции относительно оси является постоянной величиной.
расстояние от данной материальной точки до оси вращения. Момент инерции системы материальных точек зависит от распределения этих точек в пространстве. Чем ближе материальные точки находятся от оси вращения, тем меньше момент инерции данной системы. У твёрдых тел, которые можно представить как непрерывную совокупность материальных точек, момент инерции относительно оси является постоянной величиной.
Примеры решения задач
| Задание | Каким будет момент инерции системы материальных точек, которая изображена на рис.1 (а,б). Массы m и 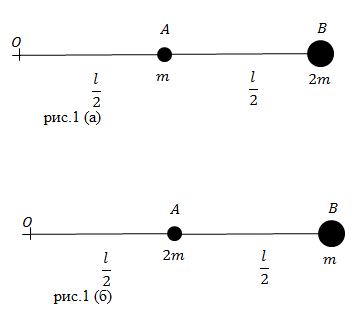
|
| Решение | Момент инерции системы из двух материальных точек (J) будет складываться из момента инерции точки A ( Рассмотрим случай изображенный на рис.1 (а). Момент инерции материальной точки относительно оси, вокруг которой она вращается равен: где расстояние от материальной точки А до оси вращения равно Момент инерции точки B будет равен: Суммарный момент инерции системы двух точек равен: Для случая рис.1 (б). Момент инерции материальной точки A относительно оси, проходящей через точку О, перпендикулярно рисунку равен: Момент инерции точки B относительно оси, проходящей через точку О: Суммарный момент инерции системы двух точек равен: |
| Ответ | a) |
| Задание | Получите выражение для кинетической энергии ( |
| Решение | Кинетическая энергия движущейся материальной точки равна по определению:
Линейная скорость точки связана с ее угловой скоростью как: Подставим выражение (2.2) формулу (2.1), имеем: |
| Ответ |











