Момент инерции тела
Определение момента инерции
Это скалярная (в общем случае тензорная) физическая величина, которая равна произведению масс материальных точек (![]() ) на которые следует провести разбиение рассматриваемого тела, на квадраты расстояний (
) на которые следует провести разбиение рассматриваемого тела, на квадраты расстояний (![]() ) от них до оси вращения:
) от них до оси вращения:
![Rendered by QuickLaTeX.com \[J=\sum^k_{i=1}{{\Delta m}_ir^2_i} \qquad (1)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-872b929258c5e9ae42ace269d5345b9f_l3.png)
В том случае, если тело можно считать непрерывным, то суммирование в формуле (1) заменяют на интегрирование, массы элементов тела обозначают как ![]() , тогда J тела, вращающегося около оси:
, тогда J тела, вращающегося около оси:
![]()
где r – функция положения материальной точки в пространстве; ![]() – плотность тела;
– плотность тела; ![]() –объем элемента тела.
–объем элемента тела.
Для однородного тела выражение (2) можно представить как:
![]()
Момент инерции в международной системе единиц измеряется в :
![]()
Величина J входит в основные законы, при помощи которых описывают вращение твердого тела.
В общем случае величина момента инерции зависит от направления оси вращения, а так как в процессе движения вектор ![]() обычно изменяет свое направление относительно тела, то момент инерции следует рассматривать как функцию времени. Исключением является момент инерции тела, вращающегося вокруг неподвижной оси. В таком случае момент инерции остается постоянным.
обычно изменяет свое направление относительно тела, то момент инерции следует рассматривать как функцию времени. Исключением является момент инерции тела, вращающегося вокруг неподвижной оси. В таком случае момент инерции остается постоянным.
Теорема Штейнера
Теорема Штейнера дает возможность вычислить момент инерции тела относительно произвольной оси вращения, когда является известным момент инерции рассматриваемого тела по отношению к оси, проходящей через центр масс этого тела и эти оси являются параллельными. В математическом виде теорема Штейнера представляется как:
![]()
где ![]() – момент инерции тела относительно оси вращения, проходящей через центр масс тела; m – масса, рассматриваемого тела; a- расстояние между осями. Обязательно следует помнить, что оси должны быть параллельны. Из выражения (4) следует, что:
– момент инерции тела относительно оси вращения, проходящей через центр масс тела; m – масса, рассматриваемого тела; a- расстояние между осями. Обязательно следует помнить, что оси должны быть параллельны. Из выражения (4) следует, что:
![]()
Некоторые выражения для вычисления моментов инерции тела
При вращении вокруг оси материальная точка имеет момент инерции равный:
![]()
где m – масса точки; r – расстояние от точки до оси вращения.
Для однородного тонкого стержня массой m и длиной l J относительно оси, проходящей через его центр масс (ось перпендикулярна стержню), равен:
![]()
Тонкое кольцо, с массой ![]() вращающееся около оси, которая проходит через его центр, перпендикулярно плоскости кольца, то момент инерции вычисляется как:
вращающееся около оси, которая проходит через его центр, перпендикулярно плоскости кольца, то момент инерции вычисляется как:
![]()
где R – радиус кольца.
Круглый однородный диск, радиуса R и массы m имеет J относительно оси, проходящей через его центр и перпендикулярной плоскости диска, равный:
![]()
Для однородного шара
![]()
где m – масса шара; R – радиус шара. Шар вращается около оси, которая проходит через его центр.
Если осями вращения являются оси прямоугольной декартовой системы координат, то для непрерывного тела моменты инерции можно вычислить как:
![]()
![]()
![]()
где ![]() – координаты бесконечно малого элемента тела.
– координаты бесконечно малого элемента тела.
Примеры решения задач
| Задание | Два шарика, которые можно считать точечными, скреплены тонким невесомым стержнем. Длина стержня l. Каков момент инерции данной системы, по отношению к оси, которая проходит перпендикулярно стержню через центр масс. Массы точек одинаковы и равны m. |
| Решение | Найдем момент инерции одного шарика ( Момент инерции второго шарика будет равен Суммарный момент инерции системы равен сумме: |
| Ответ |
| Задание | Каков момент инерции физического маятника относительно оси, которая проходит через точку O (рис.1)? Ось перепендикулярна плоскости рисунка. Считайте, что физический маятник состоит из тонкого стержня длины l, имеющего массу m и диска массы 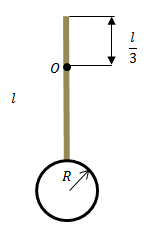
|
| Решение | Момент инерции нашего маятника (J) будет равен сумме момента инерции стержня ( Если диск вращается относительно оси, перпендикулярной его плоскости и ось проходит через его центр масс, то момент инерции равен: Диск вращается относительно оси (см. рис.1), которая находится на расстоянии: Оси параллельны, тогда в соответствии с теоремой Штейнера: Момент инерции стержня относительно оси, которая проходит через его центр масс (через середину в нашем случае) равен: По теореме Штейнера, если стержень вращается относительно точки О, то момент инерции равен: Получаем, что: |
| Ответ |











