Формула момента инерции диска
Момент инерции тела, которое можно представить в виде совокупности дискретных частиц, относительно оси вращения равен:
![Rendered by QuickLaTeX.com \[J=\sum^N_{i=1}{\Delta m_ir^2_i} \qquad (1)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-a1de0e71c06b45cba35b8702c307244a_l3.png)
где ![]() – масса i-ой материальной точки тела;
– масса i-ой материальной точки тела; ![]() – расстояние от материальной точки i до оси вращения. При рассмотрении твердого тела как сплошной среды с непрерывным распределением массы определение момента инерции заменяют следующим:
– расстояние от материальной точки i до оси вращения. При рассмотрении твердого тела как сплошной среды с непрерывным распределением массы определение момента инерции заменяют следующим:
![]()
где ![]() – элемент массы тела;
– элемент массы тела; ![]() – плотность тела;
– плотность тела; ![]() – элементарный объем.
– элементарный объем.
Момент инерции однородного диска
Рассмотрим, как находится момент инерции однородного диска, если его радиус равен R, а масса m. Ось вращения пусть проходит через центр инерции данного диска (точку О) и будет перпендикулярна его плоскости (рис.1).
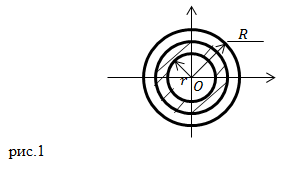
Диск можно заменить совокупностью бесконечно тонких колец, радиусы которых изменяются от нуля до R. На рис.1 выделено одно из таких колец. Рассмотрим это кольцо. Радиус его обозначим как ![]() Момент инерции данного кольца (обозначим его
Момент инерции данного кольца (обозначим его ![]() равен (см. формулу момента инерции тонкого кольца):
равен (см. формулу момента инерции тонкого кольца):
![]()
Массу данного кольца (а точнее цилиндра) можно представить как:
![]()
где ![]() – высота цилиндра. Подставим выражение для
– высота цилиндра. Подставим выражение для ![]() в формулу (3) и проведем интегрирование:
в формулу (3) и проведем интегрирование:
![Rendered by QuickLaTeX.com \[J=\int^R_0{dJ}=\int^R_0{\rho 2\pi rdrr^2dz}=2\pi \rho dz\int^R_0{r^3dr}=2\pi \rho dz{\left.\frac{r^4}{4}\right|}^R_0=\frac{\pi \rho dzR^4}{2}=\frac{mR^2}{2}\ \qquad(5)\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2ed4382334ef4506ee3831a66d2b44c0_l3.png)
где ![]() – масса диска.
– масса диска.
Если диск можно считать абсолютно тонким или он является частью цилиндра, то формула для вычисления момента инерции диска относительно оси, проходящей через его центр масс, и перпендикулярной плоскости диска, имеет вид:
![]()
В случае плоского распределения масс выполняется равенство:
![]()
где оси вращения совпадают с осями декартово системы координат. И если мы будем считать, что ось Z проходит через центр инерции диска и перпендикулярна его плоскости, то моменты инерции относительно осе X и Y будут равны:
![]()
Иногда величины моментов инерции ![]() называют моментами инерции диска относительно его диаметров.
называют моментами инерции диска относительно его диаметров.
Примеры решения задач по теме «Момент инерции диска»
| Задание | Радиус однородного диска равен R, его масса m. Каков момент инерции диска относительно оси, которая проходит через середину одного из радиусов диска, перпендикулярно его плоскости? |
| Решение | Момент инерции диска относительно оси, проходящей через его центр масс, и перпендикулярной плоскости диска, имеет равен:
Ось вокруг, которой происходит вращение нашего диска, параллельна основной, и сдвинута от нее на расстояние Подставим |
| Ответ | |
| Задание | Найти момент инерции диска относительно оси, проходящей через его центр перпендикулярно плоскости диска, если его масса m, радиус R, если в нем имеется круглое отверстие, радиус которого r. Центр отверстия находится на расстоянии d от оси диска (рис.2).
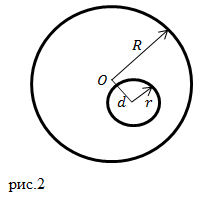
|
| Решение | Момент инерции системы (J) можно найти как:
где где Найдем соотношение между массой диска и массой части, которую вырезали. где h — толщина диска. Масса части, которую вырезали из диска, равна: Найдем отношение масс: Масса части, которую вырезали равна: Подставим выражение (2.8) в формулу (2.4), имеем: |
| Ответ | |











