Момент инерции

Определение момента инерции

Момент инерции тела по отношению к оси вращения – это мера инертности тела во вращении вокруг этой оси.

ОПРЕДЕЛЕНИЕ

Моментом инерции тела (системы тел) по отношению к оси вращения называют физическую величину, равную произведению масс материальных точек ( $\Delta m_i$ ) на которые можно разбить рассматриваемое тело на квадраты расстояний ( $r^2_i$ ) от них до оси вращения. Момент инерции обозначают буквой J, тогда определение момента инерции в математическом виде можно записать как:

$J=\sum^N_{i=1}{{\Delta m}_ir^2_i} \qquad (1)$

Если тело является непрерывным, то суммирование (1) можно свести к интегрированию, если перейти к бесконечно малым элементам тела (dm):

$J=\int_m{r^2dm=\int_V{r^2}\rho dV} \qquad (2)$

где интегрирование производят по всему объему тела. Величина r – функция положения материальной точки в пространстве; $\rho$ – плотность тела; dV – элементарный объем тела.

Единицей измерения момента инерции в международной системе единиц является:

$\left[J\right]=kg\cdot m^2$

Теорема Штейнера

Теорема Штейнера позволяет найти момент инерции тела относительно любой оси вращения, если известен момент инерции рассматриваемого тела относительно оси, которая проходит через центр масс этого тела и оси параллельны. Математическая запись теоремы Штейнера:

$J=J_0+ma^2 \qquad (3)$

где J – момент инерции тела относительно произвольной оси вращения; $J_0$ – момент инерции тела относительно оси вращения, проходящей через центр масс тела; m – масса, рассматриваемого тела; a- расстояние между осями. Обязательно следует помнить, что оси должны быть параллельны.

Получается, что момент инерции тела по отношению к оси, которая проходит через его центр масс всегда меньше, чем относительно любой другой оси, параллельной первой.

Некоторые выражения для вычисления моментов инерции тела

Если осями вращения служат оси прямоугольной декартовой системы координат, то для непрерывного тела моменты инерции можно вычислить как:

$J_{xx}=\int_m{\left(y^2+z^2\right)dm}=\int_V{\left(y^2+z^2\right)\rho dV} \qquad (4)$

$J_{yy}=\int_V{\left(x^2+z^2\right)\rho dV} \qquad(5)$

$J_{zz}=\int_V{\left(y^2+x^2\right)\rho dV} \qquad(6)$

где m – масса тела; V – объем тела; $x,y,z$ – координаты бесконечно малого элемента тела.

Если тело является однородным, то момент инерции по отношению к оси является прямо пропорциональным плотности тела и зависит от формы, размеров тела, то того как тело размещено по отношению к оси вращения.

Моменты инерции, которые находят как:

$J_{xy}=\int_m{xydm} \qquad (7)$

$J_{xz}=\int_m{xzdm} \qquad (8)$

$J_{yz}=\int_m{yzdm} \qquad (9)$

называют центробежными моментами инерции по отношению к осям прямоугольной декартовой системы координат.

Если тело является набором материальных точек, то есть не является непрерывным, то в выражениях (4-9) вместо интегрирования переходят к суммированию.

Примеры решения задач

ПРИМЕР 1

Задание

Получите формулу для момента инерции однородного шара (J), который имеет радиус R и массу m по отношению к оси, которая проходит через его центр масс.

Решение

Сделаем рисунок.

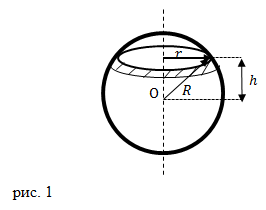
Разобьем весь шар на элементарные массы. Такой массой будет диск радиуса r, на расстоянии h от диска, который проходит через центр масс шара (точку О) (рис.1). Для таких дисков их радиус (r) связан с расстоянием (h) от главного сечения шара (круга, в котором лежит центр масс шара) (см. рис. 1):

$r^2=R^2-h^2 \qquad (1.1)$

причем величина -R $\le h\le$ R.

Момент инерции для элемента массы запишем как:

$dJ=\frac{dmr^2}{2} \qquad (1.2)$

где для рассматриваемого диска имеем:

$dm=\rho dV=\rho \pi r^2dh \qquad (1.3)$

где dh — высота рассматриваемого диска. Тогда элементарный момент инерции (используя выражения (1.2), (1.1) и (1.3)) запишем как:

$dJ=\frac{c \pi r^2dh\ r^2}{2}=\frac{c \pi r^4dh} {2}=\frac{c \pi {(R^2-h^2)}^2dh} {2} \qquad (1.4)$

Для того, чтобы найти момент инерции всего шара, относительно оси, которая проходит через его центр масс возьмем интеграл по объему шара:

$J=\int_V{dJ}=2\int^R_0{\frac{\rho \pi {(R^2-h^2)}^2dh} {2}=\frac{8\pi \rho}{15}}R^5$

Ответ

$J=\frac{8\pi \rho}{15}R^5$

ПРИМЕР 2

Задание

Каким будет момент инерции шара, который рассматривался в примере 1, относительно оси вращения, которую проведем как касательную к этому шару?

Решение

Для решения задачи воспользуемся результатом решения моментом инерции шара относительно оси вращения, которую проводили через центр масс. Обозначив этот момент инерции как $J_0$ :

$J_0=\frac{8\pi \rho}{15}R^5 \qquad (2.1)$

И будем применять теорему Шрейнера. Учитывая, что шар является фигурой симметричной, мы можем оси вращения располагать как угодно, главное, чтобы они были параллельны. Расстояние между осями по условию задачи равно радиусу шара, поэтому теорему Штейнера запишем как:

$J=J_0+mR^2=\frac{8\pi \rho}{15}R^5+\frac{4}{3}\pi \rho R^3R^2=\pi \rho R^5\left(\frac{8+20}{15}\right)=\frac{28\pi \rho R^5}{15}$