Момент инерции шара

ОПРЕДЕЛЕНИЕ

Момент инерции (J) – это физическая величина, являющаяся мерой инертности тела, вращающегося вокруг оси.

Это скалярная (в общем случае тензорная) величина. Для непрерывного однородного тела, вращающегося около оси, момент инерции определяют как:

$J=\int_m{r^2dm=\int_V{r^2}\rho dV=\rho \int_V{r^2}dV} \qquad (1)$

где r – функция положения материальной точки в пространстве; $\rho$ – плотность тела; $dV$ –объем элемента тела.

Момент инерции однородного шара

Однородный по объем шар можно представить как систему сферических слоев (или тонких дисков), обладающих массами ( $dm$ ).

По условию шар является однородным, плотность его можно представить как:

$\rho =\frac{m}{V} \qquad (2)$

где $V=\frac{4}{3}\pi R^3$ – объем всего шара; m – масса всего шара.

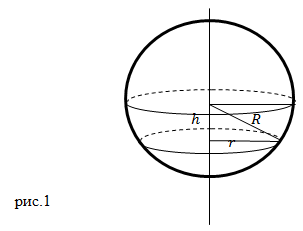
В качестве элементарной массы выберем сферический слой радиуса r (указанный на рис.1). Его массу можно представить как:

$dm=\rho dV \qquad (3)$

При этом объем рассматриваемого сферического слоя равен:

$dV=4\pi r^2dh \qquad (4)$

Момент инерции тонкого диска (толщина диска $dh\ll r$ ) равен:

$dJ=\frac{r^2dm}{2} \qquad (5)$

Выделенный нами диск находится на расстоянии h от центра шара. Радиус рассматриваемого нами диска связан с расстоянием h выражением:

$r=\sqrt{R^2-h^2} \qquad (6)$

Тогда формулу (4) преобразуем к виду:

$dV=4\pi (R^2-h^2)dh \qquad (7)$

Просуммируем моменты инерции всех дисков:

$J=\int^R_{-R}{dJ=\int^R_{-R}{\frac{4\pi {\left(R^2-h^2\right)}^2dh}{2}=}}2\pi \rho (\int^R_{-R}{R^4dh-2\int^R_{-R}{R^2h^2dh}+\int^R_{-R}{h^4dh})}=\frac{2}{5}mR^2$

Получили, что момент инерции однородного шара, относительно его диаметра равен:

$J=\frac{2}{5}mR^2 \qquad (8)$

Момент инерции полого шара (сферы)

Момент инерции сферы удобно находить, используя полярный момент инерции. Это момент инерции тела относительно некоторой точки, назовем ее O. Он равен произведению всех масс точек тела на квадраты расстояний от них до точки О. Если через полюс О провести прямоугольные оси, то полярный момент ( $J_p$ ) равен:

$J_p=\sum{m\left(x^2+y^2+z^2\right)} \qquad (9)$

Полярный момент инерции равен половине суммы моментов инерции тела относительно трех прямоугольных осей, которые проходят через полюс:

$J_p=\frac{J_x+J_y+J_z}{2}\ \qquad (10)$

В центре тяжести тела полярный момент инерции имеет минимальной значение.

Рассмотрим сферу радиуса R. Для нее удобно сначала найти полярный момент инерции относительно ее центра ( $J_p$ ):

$J_p=m\ R^2\ \qquad (11)$

Согласно формуле (10) и зная, что для сферы $J_x=J_y=J_z=J$ , имеем:

$J=\frac{2}{3}J_p\ \qquad (12)$

Получаем, что момент инерции сферы (полого шара) равен:

$J=\frac{2}{3}m\ R^2\ \qquad (13)$

Примеры решения задач

ПРИМЕР 1

Задание

Шар, массой m и радиусом R вращается около оси, проходящей через его центр. Уравнение вращения шара д: $\varphi =K+Lt^2+Nt^3$ . Запишите уравнение изменения момента сил в зависимости от времени ( $M(t)$ ).

Решение

Уравнение вращения твердого тела можно записать как:

$M=J\frac{d^2\varphi}{dt^2} \qquad (1.1)$

где момент инерции однородного шара относительно оси, проходящей через его центр равен:

$J=\frac{2}{5}mR^2 \qquad (1.2)$

$\frac{d^2\varphi}{dt^2}$ найдем, используя, уравнение $\varphi (t)$ , заданное в условии задачи:

$\frac{d^2\varphi}{dt^2}=2L+6Nt \qquad (1.3)$

Подставим (1.2) и (1.3) в (1.1), получим:

$M=\left(2L+6Nt\ \right)\frac{2}{5}mR^2$

Ответ

$M=\left(2L+6Nt\ \right)\frac{2}{5}mR^2$

ПРИМЕР 2

Задание

Какова кинетическая энергия поступательного движения однородного шара ( $E_{k1}$ ), если полная кинетическая энергия шара равна $E_k$ ? Считайте, что шар катится с постоянной скоростью без скольжения.

Решение

Сделаем рисунок.

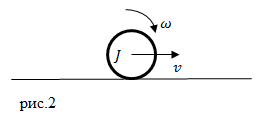
Шар в предложенной задаче совершает поступательное движение с некоторой скоростью v и вращается вокруг своей оси с угловой скоростью $\omega$ , причем:

$\omega =\frac{v}{R} \qquad (2.1)$

где R – радиус шара. Полная кинетическая энергия в нашем случае равна сумме кинетической энергии поступательного движения и кинетической энергии вращения:

$E_k=\frac{mv^2}{2}+\frac{J{\omega}^2}{2} \qquad (2.2)$