Экстремумы функции

ОПРЕДЕЛЕНИЕ

Экстремумами (максимумами и минимумами) функции называются значения функции в точках максимума и минимума.

Точки экстремума функции

Говорят, что в точке $x_{0}$ максимум (минимум), если существует такая $\delta$ -окрестность точки $x_{0}$ — $\left(x_{0} -\delta ,\; x_{0} +\delta \right)$ , что для всех $x$ из этой окрестности, отличных от $x_{0}$ выполняется неравенство $f\left(x\right)<f\left(x_{0} \right)$ $\left(f\left(x\right)>f\left(x_{0} \right)\right)$ .

ОПРЕДЕЛЕНИЕ

Точки максимума и минимума называются точками экстремума.

ОПРЕДЕЛЕНИЕ

Точки области определения, в которых производная функции равна нулю или не существует, называются критическими точками.

Необходимое условие существования экстремума функции. Пусть функция $f\left(x\right)$ дифференцируема в промежутке $\left(a,\, b\right)$ . Если в некоторой точке $x_{0} \in \left(a,\, b\right)$ функция $f\left(x\right)$ имеет экстремум, то в этой точке производная равна нулю: $f'\left(x_{0} \right)=0$ .

Достаточное условие существования экстремума функции. Если производная функции $f\left(x\right)$ равна нулю в точке $x_{0}$ и при переходе через эту точку в сторону возрастания $x$ меняет знак с «+» («-») на «-» («+»), то в точке $x_{0}$ функция имеет максимум (минимум). Если же при переходе через точку $x_{0}$ производная функции не меняет знак, то в этой точке функция $f\left(x\right)$ экстремума не имеет.

Для исследования функции на экстремум необходимо:

найти критические точки функции;
проверить, изменяет ли знак производная функции при переходе через критическую точку;
вычислить значения максимума 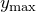$y_{\max }$ или минимума $y_{\min }$ .

Примеры исследования функции на экстремум

ПРИМЕР 1

Задание

Найти экстремум функции $y=x^{3} -3x+1$

Решение

Найдем критические точки функции, для этого вычислим производную заданной функции

$y'=3x^{2} -3,$

приравняем её к нулю и найдем корни полученного квадратного уравнения

$3x^{2} -3=0\Rightarrow x^{2} -1=0\Rightarrow \left(x-1\right)\left(x+1\right)=0\Rightarrow x_{1} =-1,\quad x_{2} =1$

Получили две критические точки $x_{1} =-1;\ x_{2} =1$ . Обозначим найденные корни на числовой оси и определим знак производной на полученных интервалах.

Пример исследования функции на экстремум

В точке $x_{1} =-1$ производная меняет знак с «+» на «-», значит в этой точке максимум. Вычислим значение максимума

$y_{\max } =y\, \left(-1\right)=\left(-1\right)^{3} -3\cdot \left(-1\right)+1=-1+3+1=3$

В точке $x_{2} =1$ производная меняет знак с «-» на «+», значит, $x_{2}$ — точка минимума. Значение минимума соответственно равно

$y_{\min } =y\, \left(1\right)=1^{3} -3\cdot 1+1=1-3+1=-1$

Ответ

$y_{\max } =3,\ y_{\min } =-1$

ПРИМЕР 2

Задание

Найти экстремум функции

$y=x^{2} -\frac{2}{x}$

Решение

Область определения функции $y=x^{2} -\frac{2}{x}$ — вся числовая прямая, за исключением точки $x=0$ , то есть $D\left(y\right):x\in \left(-\infty ;\; 0\right)\bigcup \left(0;\; +\infty \right)$ .

Вычислим производную заданной функции и найдем критические точки

$y'=2x+\frac{2}{x^{2} }$

Приравниваем к нулю производную

$2x+\frac{2}{x^{2} } =0\Rightarrow \frac{2x^{3} +2}{x^{2} } =0\Rightarrow 2\left(x^{3} +1\right)=0\Rightarrow x^{3} =-1$

Получаем одну критическую точку $x=-1$ . Обозначим на числовой оси область определения функции и найденную критическую точку и определим знак производной на полученных интервалах

В точке $x=-1$ производная меняет знак с «-» на «+», значит, в этой точке минимум. Значение минимума соответственно равно

$y_{\min } =y\, \left(1\right)=1^{2} -\frac{2}{1} =-1$

Ответ

$y_{\min } =-1$

Понравился сайт? Расскажи друзьям!