Уравнения Навье-Стокса

ОПРЕДЕЛЕНИЕ

Уравнения Навье-Стокса – это система дифференциальных уравнений, которая описывает движение вязкой ньютоновской жидкости либо газа. Так называемая «вязкость» жидкости – это её способность оказывать сопротивление, если какую-то её часть попытаться сдвинуть относительно соседнего слоя (например, при гребле). При этом в жидкости происходит внутреннее трение.

Ньютоновская жидкость – это жидкость, для которой скорость её деформации пропорциональна вязкости. Ньютоновская жидкость течет всегда, даже если силы, воздействующие на нее, очень малы – только бы они не были нулевыми. Типичная ньютоновская жидкость – вода. Вспомните, как она ведет себя в невесомости: это тот случай, когда на жидкость совсем не воздействуют внешние силы, даже сила тяжести.

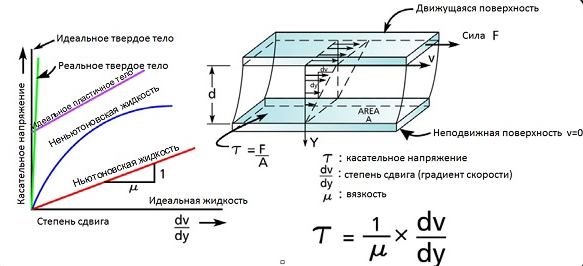
Система уравнений Навье-Стокса для несжимаемой жидкости

Система уравнений Навье-Стокса для несжимаемой жидкости, к которой с большой точностью можно отнести воду, имеет вид:

$\left\{\begin{array}{l} {\frac{\partial v_{i} }{\partial t} +v_{k} \frac{\partial v_{i} }{\partial x_{k} } =-\frac{1}{\rho } \frac{\partial p}{\partial x_{i} } +\nu \frac{\partial }{\partial x_{k} } (\frac{\partial v_{i} }{\partial x_{k} } +\frac{\partial v_{k} }{\partial x_{i} } )} \\ {\frac{\partial \rho }{\partial t} +\nabla (\rho \bar{v})=0} \end{array}\right$

Здесь $\rho$ – плотность жидкости, t – время, р – давление, $\bar{v}(v_{i} ,v_{k} )$ – проекции скорости (вектора) на координатные оси, $\mu$ – коэффициент динамической вязкости; $х_i$ , $x_k$ – пространственные координаты. $\nabla =\frac{\partial }{\partial x_{i} } \bar{i}+\frac{\partial }{\partial x_{k} } \bar{k}$ – оператор набла.

Первое уравнение в системе – это собственно уравнение движения. В левой его части стоят произведения плотности на соответствующие ускорения. В правой же части – произведения плотности на силы давления и внутреннего трения.

Второе уравнение – это уравнение неразрывности. Его физический смысл – это сохранение массы для потока жидкости.

Выражение $\frac{\partial v_{i} }{\partial t} +v_{k} \frac{\partial v_{i} }{\partial x_{k} }$ – это не что иное, как субстанциональная производная (также её называют полной). Она показывает, как изменяется ускорение материальной точки, которая движется в стационарной среде жидкости. При этом $\frac{\partial v_{i} }{\partial t}$ отображает изменение свойств точки в течение времени, как если бы она была неподвижной. $v_{k} \frac{\partial v_{i} }{\partial x_{k} }$ — конвективная производная, описывающая эволюцию свойств в неподвижной точке из-за того, что через нее со скоростью $\bar{v}$ протекает жидкая среда.

Система уравнений Навье-Стокса дает очень точные решения, если рассматривается ламинарное течение жидкости, либо геометрия каналов несложная. А вот при турбулентном течении уравнения очень чувствительны к значениям коэффициентов: изменение числа Рейнольдса на 0,05% может привести к кардинально другому результату.

На практике система уравнений Навье-Стокса применяется для расчёта конвекции и термической диффузии в теплофизике и теплотехнике; для предсказания поведения смесей, состоящих из многих компонентов. Также эта система используется для описания процессов в плазме и межзвёздном газе, течений в мантии Земли. С помощью системы уравнений Навье-Стокса делают прогноз погоды, предсказывая движение масс воздуха в атмосфере.

Примеры решения задач

ПРИМЕР 1

Задание

Рассмотрим плоское течение жидкой среды. Будем считать, что жидкость несжимаемая. Докажите, что такое поле скоростей удовлетворяет уравнению неразрывности:

$v_{x} =\frac{A(x ^2 -y^2 )}{r^4 }$

$v_{y} =\frac{2Axy }{r^4 }$

$v_{z} =0$

$r^2 =x^2 +y^2$

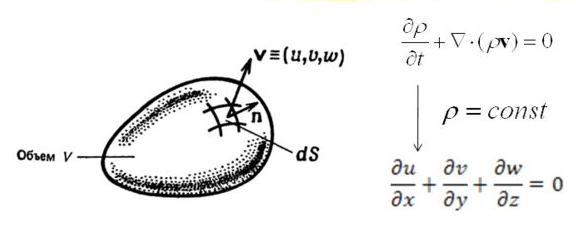
Решение

Уравнение неразрывности из системы уравнений Навье-Стокса имеет вид:

$\frac{\partial \rho }{\partial t} +\nabla (\rho \bar{v})=0$

Для несжимаемой жидкости плотность $\rho$ постоянна, и уравнение неразрывности можно преобразовать:

$div( \bar{v})=0$

Последнее выражение можно переписать в виде:

$\frac{\partial v_{x} }{\partial x} +\frac{\partial v_{y} }{\partial y} +\frac{\partial v_{z} }{\partial z} =0$

$\frac{\partial \left(\frac{A(x ^2 -y^2 )}{r^4 } \right)}{\partial x} +\frac{\partial \left(\frac{2Axy }{r^4 } \right)}{\partial y} +0=\frac{\partial \left(\frac{A(x ^2 -y^2 )}{(x^2 +y^2 )^2 } \right)}{\partial x} +\frac{\partial \left(\frac{2Axy }{(x ^2 +y ^2 )^2 } \right)}{\partial y} =$

$=A\left(\frac{-4x(x ^2 -y^2 )}{(x^2 +y^2 )^3 } +\frac{2x}{(x^2 +y^2 )^2 } \right)+A\left(\frac{2x}{(x^2 +y^2 )^2 } -\frac{8xy^2 }{(x^2 +y^2 )^3 } \right)=0$

Таким образом, заданное поле скоростей удовлетворяет уравнению неразрывности несжимаемой жидкости.

Ответ

Поле скоростей отвечает уравнению неразрывности.

ПРИМЕР 2

Задание

Определить функцию давления p(x,y) для плоского течения несжимаемой жидкости с постоянной вязкостью в отсутствии массовых сил по заданному полю скоростей $v_x=2x,\ v_y=-2y$ .

Решение

$\left\{\begin{array}{l} {\frac{\partial v_{x} }{\partial t} +v_{y} \frac{\partial v_{x} }{\partial y} =-\frac{1}{\rho } \frac{\partial p}{\partial y} +\nu \frac{\partial }{\partial y} (\frac{\partial v_{x} }{\partial y} +\frac{\partial v_{y} }{\partial x} )} \\ {\frac{\partial v_{y} }{\partial t} +v_{x} \frac{\partial v_{y} }{\partial x} =-\frac{1}{\rho } \frac{\partial p}{\partial x} +\nu \frac{\partial }{\partial x} (\frac{\partial v_{y} }{\partial x} +\frac{\partial v_{x} }{\partial y} )} \\ {\frac{\partial \rho }{\partial t} +\nabla (\rho \bar{v})=0} \end{array}\right$

Мы заменили индексы i, k при составляющих скорости мы заменили более привычными x, y – так, как было записано в условии задачи. При этом мы смогли заменить пространственные координаты $x_{i}$ , $x_{k}$ на удобные x, y. Суть же уравнения не изменилась.

Перепишем систему уравнений Навье-Стокса, учитывая особенности исследуемой модели жидкости:

$\left\{\begin{array}{l} {\frac{\partial v_{x} }{\partial t} +v_{x} \frac{\partial v_{x} }{\partial x} +v_{y} \frac{\partial v_{x} }{\partial y} =-\frac{1}{\rho } \frac{\partial p}{\partial y} +\nu \Delta v _{x} } \\ {\frac{\partial v_{y} }{\partial t} +v_{y} \frac{\partial v_{y} }{\partial y} +v_{x} \frac{\partial v_{y} }{\partial x} =-\frac{1}{\rho } \frac{\partial p}{\partial x} +\nu \Delta v_{y} } \\ {\frac{\partial v_{x} }{\partial x} +\frac{\partial v_{y} }{\partial y} =0} \end{array}\right$

Последнее уравнение, являющееся выражением закона неразрывности для несжимаемой жидкости выполняется автоматически для заданного поля скоростей. Два первых уравнения перепишутся в виде:

$\begin{array}{l} {\frac{dp }{dx } =-4\rho x ,} \\ {\frac{dp }{dy } =-4\rho y .} \end{array}$