Основное уравнение молекулярно-кинетической теории газов
Определение и формула основного уравнения молекулярно-кинетической теории
Изучать процессы, которые протекают в больших системах весьма сложно из за огромного числа частиц и их малых размеров. Рассмотреть отдельно каждую частицу практически невозможно, вводятся статистические величины: средняя скорость частиц, их концентрация, масса частицы. Возникает необходимость, установления математической связи (уравнения) между микро параметрами, которые относят к отдельным частицам (масса молекулы, ее скорость и т.д.) и макро параметрами описывающими систему в целом (температура, давление) Формула, характеризующая состояние системы с учетом микроскопических и макроскопических параметров, называется основным уравнением молекулярно-кинетической теории газов (МКТ).
Естественно, что проще всего устанавливается такая связь на простейшей модели — идеальном газе. В газе молекулы совершают свободное (изолированное от других молекул) движение, лишь время от времени сталкиваясь друг с другом или со стенками сосуда. Было сделано предположение, что давление газа является результатом ударений молекул о стенки сосуда. В свою очередь, сила есть импульс, передаваемый от тела к телу в секунду. Значит, чтобы найти давление газа, нужно определить, какой импульс передаёт газ единице площади стенки сосуда в секунду.
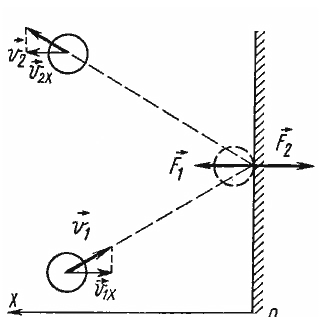
рис. 1.
Довольно простой расчет и основные положения молекулярно-кинетической теории позволяют получить уравнение, связывающее давление газа, если известны масса молекулы ![]() , среднее значение скорости молекул
, среднее значение скорости молекул ![]() и концентрацию молекул в газе n:
и концентрацию молекул в газе n:
![]()
это уравнение называют основным уравнением молекулярно-кинетической теории.
Если мы обозначим среднее значение кинетической энергии поступательного движения молекул через ![]() , в таком случае уравнение (1) примет вид:
, в таком случае уравнение (1) примет вид:
![]()
Средняя кинетическая энергия молекулы пpи равновесии идеального газа обладает одной очень важной особенностью: в смеси различных идеальных газов средняя кинетическая энергия молекулы для различных компонентов смеси одна и та же.
Примеры решения задач
| Задание | Считая воздух идеальным газом, определите скорость теплового движения молекул при нормальны условиях. |
| Решение | Для решения поставленной задачи используем основное уравнение молекулярно-кинетической теории газов:
из определения плотности вещества: где N- число молекул воздуха получаем: где по определению концентрации молекул вещества Переписываем основное уравнение молекулярно-кинетической теории в удобных для нас параметрах: отсюда используем для расчета величины скорости теплового движения воздуха при нормальных условиях общеизвестную справочную информацию, так получим: давление воздуха:
расчет дает следующее: |
| Ответ | Скорость теплового движения молекул воздуха при нормальных условиях составляет |
| Задание | Имеется поток молекул массы а) число ударов молекул N за секунду о единицу поверхности плоской стенки, нормаль к которой образует угол б) какова температура газа в этом потоке? |
| Решение | Сделаем рисунок
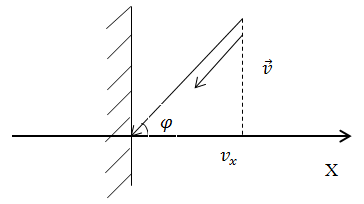
рис. 2. 1) Найдем число столкновений молекул о площадку с единичной площадью стенки в секунду, если скорость молекулы равна 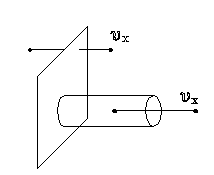
рис. 3. Наоборот, все молекулы, попадающие в цилиндр, проходя за секунду путь, равный 2) Для решения поставленной задачи используем основное уравнение МКТ:
из этих уравнений следует: |
| Ответ | 1. Число ударов молекул N за секунду о единицу поверхности плоской стенки 2. Температура в потоке газа |











