Формула уравнения Бернулли
![Rendered by QuickLaTeX.com \[ \frac{\rho v^{2}}{2} + \rho gh + p = \text{Const} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-91d6dac6b7eaba9c226a7b109dfa05ed_l3.png)
Здесь ![]() – плотность жидкости;
– плотность жидкости; ![]() – скорость течения. Слагаемое
– скорость течения. Слагаемое ![]() – динамическое давление;
– динамическое давление; ![]() – гидростатическое давление;
– гидростатическое давление; ![]() – давление жидкости на поверхность обтекаемого ею тела, по сути статическое давление.
– давление жидкости на поверхность обтекаемого ею тела, по сути статическое давление.
Проанализировав уравнение Бернулли для горизонтальной трубки тока можно сделать выводы, что при течении жидкости по горизонтальной трубе, владеющей различными сечениями, в узких местах давление на стенки трубы меньше, но скорость жидкости больше, статическое давление больше в широких местах, то есть там, где скорость меньше.
Примеры решения задач по теме «Уравнение Бернулли»
| Задание | В широкой части горизонтальной трубы вода течет со скоростью 0,5 м/с . Найти скорость течения жидкости в узкой части трубы, если разница давлений в широкой и узкой ее частях 1,33 кПа. Плотность воды |
| Решение | Сделаем рисунок
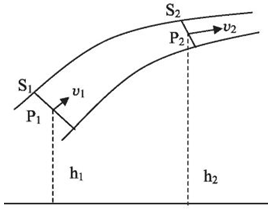
Общий вид формулы Бернулли В условии сказано, что труба горизонтальная и жидкость одинаковая Формула Бернулли упрощается к виду: Из формулы выводим значение скорости: Следовательно: Найдем численные значения:
|
| Ответ | Скорость течения жидкости в узкой части трубы 1,7 м/с. |
| Задание | В дождевальной установке вода подается сначала по трубе диаметром |
| Решение | Уравнение неразрывности:
Уравнение Бернулли: Найдем численные значения:
|
| Ответ | Статическое давление в узкой части трубы 340,2 кПа. |






![Rendered by QuickLaTeX.com \[ v_{1}=\sqrt{\frac{\rho_{2} v_{2}^{2} + 2 \Delta p}{\rho_{1}}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d7adced21d1200c9b325f597792c8659_l3.png)
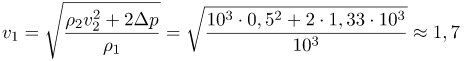 (м/с)
(м/с)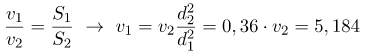 (м/с)
(м/с)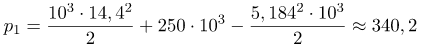 (кПа)
(кПа)




