Волновое уравнение
Природа волнового процесса
Волновой процесс может иметь самую разнообразную природу: в виде волн распространяются свет и звуковое поле, волновую природу имеют колебания вероятности и механические движения таких объектов, как струна. Электромагнитные волны используются в быту (сотовая связь, радиотехника, СВЧ-печи), в медицине (рентгеновские аппараты), в промышленности и науке (электромагнитные системы управления, лазеры и даже гамма-телескопы).
Волновой процесс отличается от колебательного тем, что изменяющаяся величина перемещается, «оторвавшись» от своего источника. Обычно при волновом движении переносится только энергия, однако в отдельных случаях (излучение газа в вакуум, процессы горения) имеет место и перенос массы.
Волновое дифференциальное уравнение
Описывать волны сложно: для них не всегда можно выделить даже общие свойства. Движение волны описывается с помощью волнового дифференциального уравнения:
![]()
В этом уравнении u – величина, которая изменяется, v – скорость волны, x, y, z и t – пространственная и временная координата.
Решение волнового уравнения
Решение этого уравнение может оказаться весьма сложным. Поэтому на практике часто используют его частное решение – уравнение плоской волны. Это волна с фронтом в виде бесконечной плоскости, движущаяся перпендикулярно своему фронту.

В природе плоских волн не существует, однако эту модель удобно использовать для расчётов. А излучение лазера или зеркальной антенны с достаточной точностью можно считать плоским.
Уравнение плоской волны гармоническое и выглядит вот так:
![]()
Здесь А – изменяющаяся величина, А0 – ее амплитуда, ![]() – начальная фаза колебаний. Волновое число k можно рассчитать, зная длину волны
– начальная фаза колебаний. Волновое число k можно рассчитать, зная длину волны ![]() :
:
![]()
Циклическая частота связана со скоростью фронта ![]() :
:
![]()
А скорость фронта волны, в свою очередь, связана с частотой:
![]()
Чтобы математически описать распространение звука, работу антенны или лампы накаливания, удобно использовать уравнение сферической волны:
![]()
Здесь r – радиус (симметричная координата), а ![]() — амплитуда сферической волны.
— амплитуда сферической волны.
Примеры решения задач
| Задание | Плоская волна распространяется с периодом 1,2 с и скоростью 15 м/с. Амплитуда колебаний равна 2 см. Когда от начала колебаний прошло 4 с, оказалось, что точка, находящаяся на 45 м от источника, сместилась на некоторое значение |
| Решение | В уравнение плоской волны выразим циклическую частоту через период (при этом начальная фаза равна нулю):
Нужно выразить волновое число через известные величины: Тогда получим формулу: Внесем в уравнение численные величины:
|
| Ответ |
| Задание | Есть упругая однородная среда, в которой распространяются две волны: одна вдоль оси абсцисс, другая вдоль оси ординат. Их движение задано уравнениями: |
| Решение | Для волн работает принцип суперпозиции, поэтому уравнение результирующего процесса – это сумма двух сложенных уравнений:
Можем заметить, что формула равна 0 (то есть колебания отсутствуют) в точках, где Выразим волновое число через длину волны: На рисунке эти прямые показаны пунктиром. 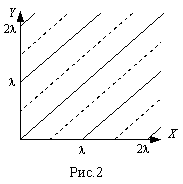
А если На рисунке эти точки показаны как сплошные линии. |
| Ответ | Отсутствие колебаний – точки |











