Радиус вписанной окружности треугольника

Определение и формула радиуса вписанной окружности в треугольник

ОПРЕДЕЛЕНИЕ

Окружность, касающаяся всех трех сторон треугольника, называется его вписанной окружностью.

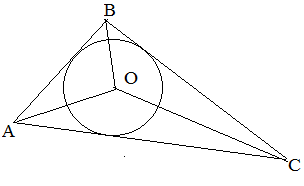
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.

Радиус вписанной окружности в треугольник равен отношению площади треугольника к его полупериметру:

$r=\frac{S}{p}$

ПРИМЕР 1

Задание	Площадь треугольника $ABC$ равна $32$ см $^{2}$ . Найдите периметр треугольника $ABC$ , если радиус вписанной окружности равен $4$ см.
Решение	Так как радиус вписанной окружности равен отношению площади треугольника к его полупериметру, то периметр треугольника находится следующим образом: $P=\frac{2S}{r} =\frac{64}{4} =16\ cm$
Ответ	$P=16$ см

ПРИМЕР 2

Задание

В прямоугольном треугольнике 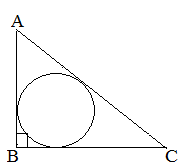$ABC$ с прямым углом $B$ катеты равны $8$ см и $6$ см. Найти радиус окружности, вписанной в треугольник $ABC$ .

Решение

Радиус вписанной окружности равен отношению площади треугольника к его полупериметру $r=\frac{S}{p}$ . Найдем площадь прямоугольного треугольника $ABC$ как площадь прямоугольного треугольника:

$S_{ABC} =\frac{1}{2} AB\cdot BC=\frac{1}{2} \cdot 8\cdot 6=24\ cm^2$